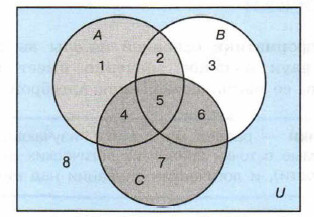
§ 17. Некоторые сведения из теории множеств

Самое главное

Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.

Пересечением двух множеств X и Y называется множество их общих элементов.

Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.

Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.

Мощностью конечного множества называется число его элементов.

Формула включений-исключений позволяет вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).

Вопросы и задания

1. Если множество X — это множество натуральных чисел, делящихся нацело на 2, а Y — множество натуральных чисел, делящихся нацело на 3, то что будет:

1) пересечением этих множеств;

2) объединением этих множеств?

2. Пусть множество X — это множество натуральных чисел, делящихся нацело на 18, а Y — множество натуральных чисел, делящихся нацело на 14. Укажите наименьшее число, входящее:

1) в пересечение этих множеств;

2) в объединение этих множеств?

3. Пусть А, В и С — некоторые множества, обозначенные кругами, U — универсальное множество.

С помощью операций объединения, пересечения и дополнения до универсального множества выразите через А, В и С следующие множества:

1) 1 ∪ 2 ∪ 3 ∪ 4 ∪ 5 ∪ 6;
2) 2 ∪ 5;
3) 5;
4) 2 ∪ 4 ∪ 5 ∪ 6;
5) 1 ∪ 2 ∪ 3;
6) 8.

4. В первую смену в лагере «Дубки» отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. При этом 10 человек были и отличниками, и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличниками, и спортсменами, и победителями олимпиад. Сколько ребят отдыхало в лагере?

5. Старшеклассники заполняли анкету с вопросами об экзаменах по выбору. Оказалось, что выбрали они информатику, физику и обществознание. В классе 38 учеников. Обществознание выбрал 21 ученик, причём трое из них выбрали ещё и информатику, а шестеро — ещё и физику. Один ученик выбрал все три предмета. Всего информатику выбрали 13 учеников, пятеро из которых указали в анкете два предмета. Надо определить, сколько же учеников выбрали физику.

*6. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Сколько человек знают все три языка?