|
|
|
|
|
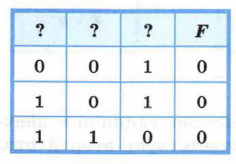
§ 19. Таблицы истинности 19.2. Анализ таблиц истинностиВ исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (23) строк. Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7. Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110). Построим по этим данным вторую часть таблицы истинности:
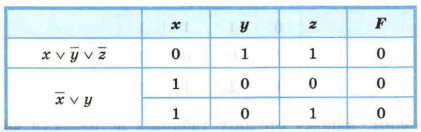
Теперь выясним, при каких значениях х, у, z логическое выражение ложно:
Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, a z может быть и 0, и 1.
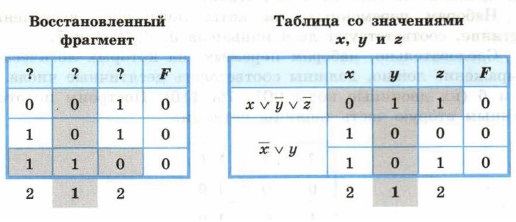
Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.
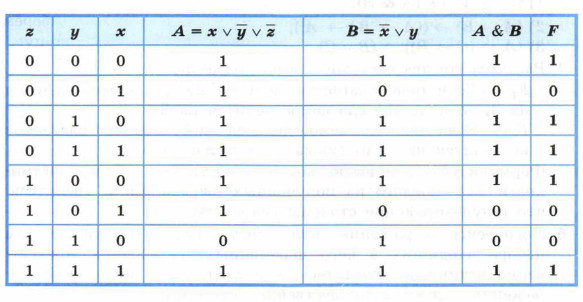
Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы. Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:
|
|
|



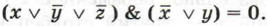 Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:
Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу: