|
|
|
|
|
§ 20. Преобразование логических выражений Основные законы алгебры логикиСпособ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики. Приведём основные законы алгебры логики. 1. Переместительные (коммутативные) законы:
2. Сочетательные (ассоциативные) законы:
3. Распределительные (дистрибутивные) законы:
4. Законы идемпотентности (отсутствия степеней и коэффициентов):
5. Закон противоречия:
6. Закон исключённого третьего:
7. Закон двойного отрицания:
8. Законы работы с константами:
9. Законы де Моргана:
10. Законы поглощения:
Справедливость законов можно доказать построением таблиц истинности.
Последовательно применим дистрибутивный закон и закон исключённого третьего:
Пробуйте самостоятельно доказать один из этих законов с помощью кругов Эйлера.
На числовой прямой даны отрезки В = [2; 12] и С = [7; 18]. Каким должен быть отрезок А, чтобы предикат Преобразуем исходное выражение, избавившись от импликации:
А, В и С — множества. Для них можем записать:
Известно, что Будем считать, что Множество В — это отрезок [2; 12]. Множество
Пересечением этих множеств будет служить промежуток [2; 7[. В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.
Для какого наименьшего неотрицательного целого десятичного числа а выражение
тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел. Прежде всего, вспомним, что представляет собой поразрядная конъюнкция двух целых десятичных чисел, например 27 и 22. 27 = 110112, 22 = 101102.
Обратите внимание на то, что если в некотором бите хотя бы одного сомножителя есть 0, то 0 есть и в этом бите результата, а 1 в результате получается только тогда, когда в соответствующих битах каждого сомножителя есть 1.
|
|
|



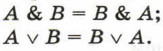
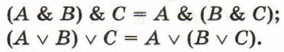
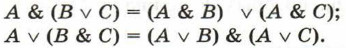
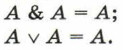
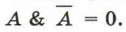
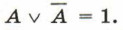
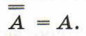
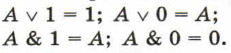
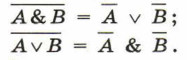
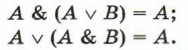
 Пример 1. Упростим логическое выражение
Пример 1. Упростим логическое выражение

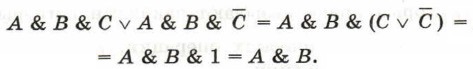
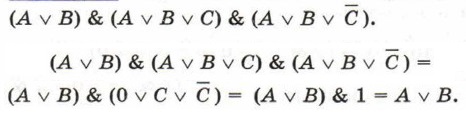
 Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:
Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:
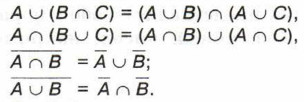
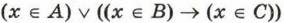 становился истинным высказыванием при любых значениях х.
становился истинным высказыванием при любых значениях х.
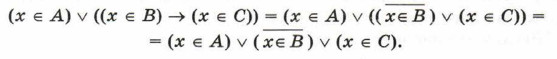

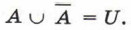
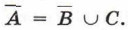 Тогда
Тогда 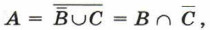 причём это минимально возможное множество А.
причём это минимально возможное множество А.
 — это промежутки ]-∞; 7[ и ]18; +∞[.
— это промежутки ]-∞; 7[ и ]18; +∞[.

 Пример 4.
Пример 4.

