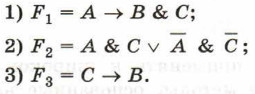Использование таблиц истинности для решения логических задач

Аппарат алгебры логики позволяет применять к широкому классу логических задач универсальные методы, основанные на формализации условий задачи.

Одним из таких методов является построение таблицы истинности по условию задачи и её анализ. Для этого следует:

1) выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами;

2) записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций;

3) построить таблицу истинности для полученных логических выражений;

4) выбрать решение — набор логических переменных (элементарных высказываний), при котором значения логических выражений соответствуют условиям задачи;

5) убедиться, что полученное решение удовлетворяет всем условиям задачи.

Пример 6. Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:

1) если А получит максимальную прибыль, то максимальную прибыль получат В и С;

2) А и С получат или не получат максимальную прибыль одновременно;

3) необходимым условием получения максимальной прибыли подразделением С является получение максимальной прибыли подразделением В.

По завершении года оказалось, что одно из трёх предположений ложно, а остальные два истинны.

Выясним, какие из названных подразделений получили максимальную прибыль.

Рассмотрим элементарные высказывания:

А — «А получит максимальную прибыль»;
В — «В получит максимальную прибыль»;
С — «С получит максимальную прибыль».

Запишем на языке алгебры логики прогнозы, высказанные экономистами:

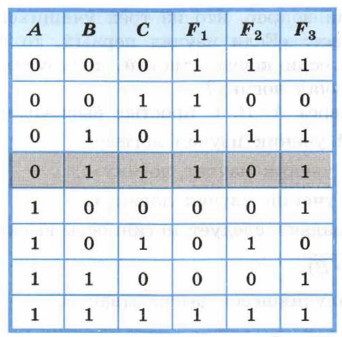
Составим таблицу истинности для F₁, F₂, F₃.

Теперь вспомним, что из трёх прогнозов F₁, F₂, F₃ один оказался ложным, а два других — истинными. Эта ситуация соответствует четвёртой строке таблицы.

Таким образом, максимальную прибыль получили подразделения В и С.