Метод рассуждений

Исходными данными в логических задачах являются высказывания. При этом высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов бывает достаточно трудно.

Основная идея этого метода состоит в том, чтобы последовательно анализировать всю информацию, имеющуюся в задаче, и делать на этой основе выводы.

Пример 1. На одной улице стоят в ряд 4 дома, в каждом из них живёт по одному человеку. Их зовут Василий, Семён, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что:

1) столяр живёт правее охотника;
2) врач живёт левее охотника;
3) скрипач живёт с краю;
4) скрипач живёт рядом с врачом;
5) Семён не скрипач и не живёт рядом со скрипачом;
6) Иван живёт рядом с охотником;
7) Василий живёт правее врача;
8) Василий живёт через дом от Ивана.

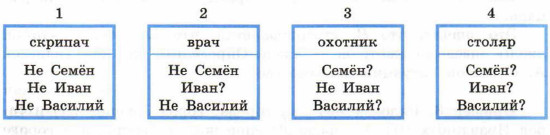
Определим, кто где живёт.

Изобразим дома прямоугольниками и пронумеруем их:

Известно, что скрипач живёт с краю (3). Следовательно, он может жить в доме 1 или в доме 4.

Скрипач живёт рядом с врачом (4), т. е. врач может жить правее (дом 2) или левее (дом 3) скрипача.

Но врач живёт левее охотника (2), следовательно, скрипач не может жить в доме 4, т. к. в противном случае получится, что врач, живущий с ним рядом, живёт правее охотника, а это противоречит условию (2). Таким образом, скрипач живёт в доме 1, а врач — рядом с ним, в доме 2.

Так как врач живёт левее охотника (2), а столяр — правее охотника (1), то охотнику достаётся дом 3, а столяру — дом 4.

Так как Семён не скрипач и не живёт рядом со скрипачом (5), то он может жить в доме 3 или в доме 4.

Так как Иван живёт рядом с охотником (6), то он может жить в доме 2 или 4.

Так как Василий живёт правее врача (7), то он может жить в доме 3 или 4.

Подводим итоги с учётом того, что Василий живёт через дом от Ивана (8): в доме 1 может жить только Геннадий, в доме 2 — Иван, в доме 4 — Василий, в доме 3 — Семён.

Как видите, далеко не самая сложная задача потребовала достаточно серьёзных рассуждений. Этот метод, как правило, применяется для решения простых задач.