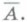|
|
|
|
|
§ 1.3. Элементы алгебры логики 1.3.2. Логические операции (продолжение)Дизъюнкция. ИнверсияРассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использова ния в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
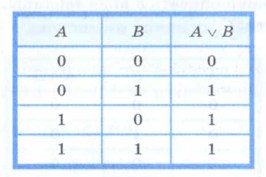
Для записи дизъюнкции используются следующие знаки: ИЛИ, ∨, |, +. Например: А ИЛИ В, A∨B, А|В, А+В. Дизъюнкция определяется следующей таблицей истинности:
Инверсия
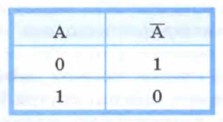
Для записи инверсии используются следующие знаки: НЕ, ¬, —. Например: НЕ А, ¬ А, Инверсия определяется следующей таблицей истинности:
Инверсию также называют логическим отрицанием. Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 8-х классов — отличники» является высказывание «Неверно, что все юноши 8-х классов — отличники», другими словами, «Не все юноши 8-х классов — отличники». Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что ...», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не». Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
|
|
|



 Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
 Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.