|
|
|
|
|
§ 1.1. Системы счисления 1.1.2. Двоичная система счисленияДвоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1. На основании формулы (1) для целых двоичных чисел можно записать: аn-1аn-2...а1а0 = an-1 • 2n-1 + аn-2 • 2n-2 +...+ а0 • 20. (1') Например: 100112 = 1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 1 • 20 = 24 + 21 + 20 = 1910.
Разделим аn-1 • 2n-1 + аn-2 • 2n-2 + ... + а0 • 20 на 2. Частное будет равно аn-1 • 2n-2 + ... + а1, а остаток будет равен а0. Полученное частное опять разделим на 2, остаток от деления будет равен а1. Если продолжить этот процесс деления, то на n-м шаге получим набор цифр: а0, а1, а2, ... аn-1,. которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2. Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
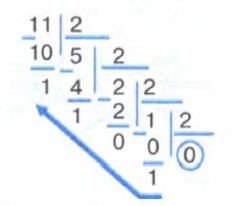
Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.
36310 = 1011010112
|
|
|



 Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
 Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1').
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1').
 Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так: