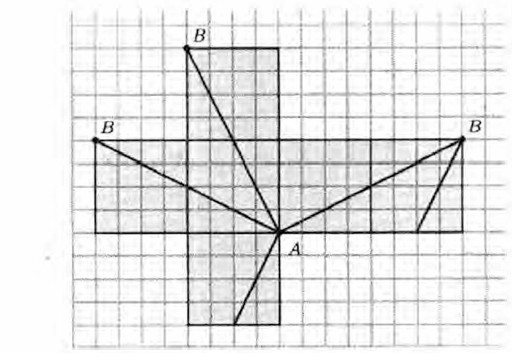
Сравнение дробей. Домашние работы (окончание)

953. Для нахождения кратчайшего пути нужно сделать развертку куба.

954. а) 5 = 2 • 2 + 1; в) 29 = 9 • 3+2; б) 100 = 30 • 3+10; г) 100 = 11 • 9 + 1.

962. Так как 6 литров составляют 6 частей аквариума, то одна часть аквариума равна 1 литру, а всего аквариум вмещает 1 • 7 = 7 л воды.

963. а) Если радиус круга 3 дм, то его диаметр 2r = 2 • 3 = 6 дм. Так как 6 дм > 4 дм, то из прямоугольного листа фанеры размерами 6 дм х 4 дм круг радиуса 3 дм вырезать нельзя; б) при r = 2 дм ⇒ d = 2г = 4 дм, 4 дм < 4 дм < 6 — круг можно вырезать; в) при r = 1 дм ⇒ d = 2r = 2 дм, 2 дм < 4 дм < 6 дм — круг можно вырезать.

964. 1) 229372 : 286 • 506 = 802 • 506 = 405812;
2) 282370 : 302 : 85 = 935 : 85 = 11;
3) 195 840 : (32 • 18) = 195 840 : 576 = 340;
4) 538 • (301608 : 426) = 538 • 708 = 380 904.

968. а) 2800 : 4 = 700 г;
б) 2800 : 4 • 3 = 700 • 3 = 2100 г = 2 кг 100 г;
в) 2800 : 7 • 2 = 400 • 2 = 800 г;
г) 2800 : 7 • 5 = 400 • 5 = 2000 г = 2 кг.

969. Площадь всего участка равна 40 • 15 = 600 м².

970. Мотоциклисты встретятся через 348 : (62 + 54) - 348 : 116 = 3 часа.

971. а) 4 • 380 = 1520 г > 9 • 125 = 1125 г; б) 22 • 125 = 2750 г > 7 • 380 = 2660 г.

972. а) 3 • 910 = 2730 г < 4 • 780 = 3120 г; б) 8 • 780 = 6240 г < 7 • 910 = 6370 г.

973. а) b + с соответствует общей длине отрезанной проволоки; б) а — (b + с) соответствует длине оставшейся проволоки; в) а - b соответствует длине проволоки, оставшейся после отрезания; г) а - b - с = а - (b + с) соответствует общей длине отрезанной проволоки.
При а = 45, b = 7, с = 12; а - (b + с) = 45 - (7 + 12) = 45 - 19 = 26, а - b - с = 45 - 7 - 12 = 38 - 12 - 26.

<<< К началу