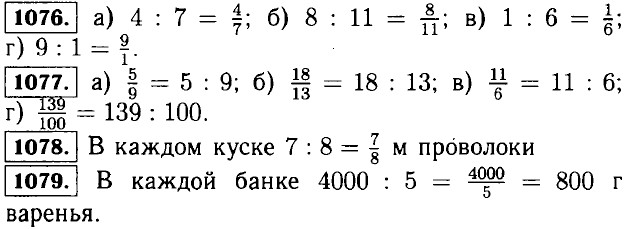Деление и дроби. Домашние работы (окончание)

1071. Четверо детей могли выбрать напитки 4! = 1 • 2 • 3 • 4 = 24 способами.

1072. а) при b = 19, q = 64, r = 18; a = bq + r = 19 • 64 + 18 = 1216 - 1 - 18 = 1234; б) при а = 567, q = 37, r = 12; b = (а - r) : q = (567 - 12) : 37 = 555 : 37 = 14; в) при а = 361, b = 25, r = 11; q= (a - r) : b= (361 - 11) : 25 = 350 : 25 = 14.

1073. 1) Пусть подводная лодка двигалась на поверхности воды х ч, тогда под водой она находилась 20x ч. Под водой лодка находилась на (20x - х) ч больше, чем на поверхности. Составим и решим уравнение: 20x - х = 57 ⇒ х = 57 : 19 = 3ч лодка находилась на поверхности, а под водой она находилась 20 : 3 = 60 ч.
2) Пусть подводная лодка прошла на поверхности воды у км , тогда под водой она прошла 17у км. Под водой лодка прошла на (17у - у) км больше, чем но поверхности. Составим и решим уравнение: 17у - у = 320 ⇒ у - 320 : 16 = 20 км лодка прошла на поверхности воды, а под водой она прошла 17 • 20 = 340 км.

1074. а) 2738 = 125 • 21 + 113; б) 3049 = 134 • 22+101.

1075. Надо использовать несколько изоляторов.

1080. Первая бригада вспахала 8 • 48 = 384 га. Вторая бригада вспахивала 762 - 384 = 378 га, а за день она вспахивала 378 : 9 = 42 га. Значит первая бригада вспахала на 384 - 378 = 6 га больше, чем вторая.

1081. Пусть скорость второго поезда х км/ч, тогда скорость первого поезда (х + 10) км/ч. Скорость сближения поездов равна (х + х + 10) км/ч, они встретились через 784 : (х + х + 10) ч. Составим и решим уравнение: 784 : (х + х + 10) = 8 ⇒ 2х + 10 = 784 : 8 ⇒ х = (98 - 10) : 2 = 44 км/ч - скорость второго поезда, а скорость первого поезда равна 44 + 10 = 54 км/ч.

1082. а) 874267 = 301 • 2904 + 163; б) 765 420 = 532 • 1463 + 271.

1083. 78 • 96 + 17 = 7488 + 17 = 7505.

<<< К началу