|
|
|
|
|
§ 5. Обыкновенные дроби 27. Деление и дробиРазделим 2 одинаковых яблока между тремя детьми. Число 2 не делится нацело на 3. Поэтому разделим каждое яблоко на 3 равные части и дадим каждому ребёнку по одной части от каждого яблока. Каждая часть — это
Дробь
С помощью дробей можно записать результат деления двух любых натуральных чисел.
Например,
Запишем число 3 в виде дроби со знаменателем 5. Для этого надо найти такое число, при делении которого на 5 получилось бы 3. Таким числом является 3 • 5, то есть 15. Значит,
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем.
Мы знаем, что
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные. Например: 9603 : 3 = (9000 + 600 + 3) : 3 = 9000 : 3 + 600 : 3 + 3 : 3 = 3000 + 200 + 1 = 3201.
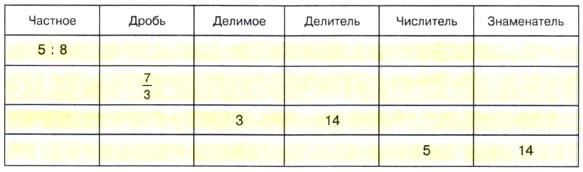
1051. Запишите в виде дроби частные: 2:5; 1 : 10; 15 : 8; 7:1; 20 : 4; 77 : 10. 1052. Запишите каждую из дробей 1053. Заполните пустые клетки таблицы:
1054. За неделю израсходовано 3 кг сахара. Сколько килограммов сахара в среднем расходовали за один день?
|
|
|



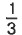 яблока, а две такие части — это
яблока, а две такие части — это 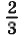 яблока. Значит, каждый ребёнок получит
яблока. Значит, каждый ребёнок получит 
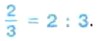

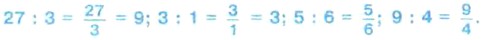

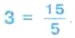

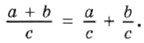 По-другому это равенство можно записать так:
По-другому это равенство можно записать так:
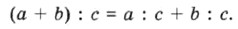


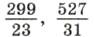 в виде частного и найдите его значение.
в виде частного и найдите его значение.