|
|
|
|
|
§ 6. Десятичные дроби. Сложение и вычитание десятичных дробей 31. Сравнение десятичных дробейПусть длина отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу:
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной. Например,
Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360. Запишем их в виде неправильных дробей:
У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель. Так как 5345 < 5360, то
Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
Десятичные дроби можно изображать на координатном луче так же, как и ; обыкновенные дроби.
Равные десятичные дроби изображаются на координатном луче одной и той же точкой. Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141).
Меньшая десятичная дробь лежит на координатном луче левее большей, и ббльшая — правее меньшей.
Например, 0,4 < 0,6 < 0,8, поэтому точка 4(0,4) лежит левее точки 8(0,6) а точка С(0,8) лежит правее точки 8(0,6) (см. рис. 141).
1172. Напишите десятичную дробь: а) с четырьмя знаками после запятой, равную 0,87;
1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях: 1,8; 13,54 и 0,789. 1174. Запишите короче дроби: 2,5000; 3,02000; 20,010.
1175. Сравните числа: 85,09 и 67,99; 55,7 и 55,7000; 0,5 и 0,724; 0,908 и 0,918; 7,6431 и 7,6429; 0,0025 и 0,00247. 1176. Расставьте в порядке возрастания числа: 3,456; 3,465; 8,149; 8,079; 0,453. А числа 0,0082; 0,037; 0,0044; 0,08; 0,0091 расставьте в порядке убывания. 1177. Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки А(0,1), B(0,5), С(0,9), D( 1,2), E(1,7).
|
|
|



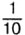 дм, то то 6 см =
дм, то то 6 см = 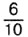 дм. Значит, АВ = 0,6 дм. Так как 1 мм =
дм. Значит, АВ = 0,6 дм. Так как 1 мм = 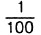 , тo 60 мм =
, тo 60 мм = 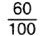 дм. Значит, АВ = 0,60 дм.
дм. Значит, АВ = 0,60 дм.
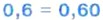

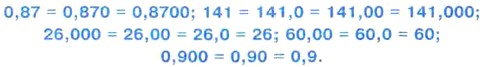
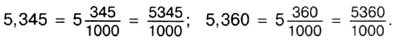
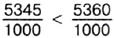 , а значит, 5,345 < 5,360, то есть 5,345 < 5,36.
, а значит, 5,345 < 5,360, то есть 5,345 < 5,36.


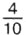 . Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку 4(0,4) (рис. 141).
. Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку 4(0,4) (рис. 141).


