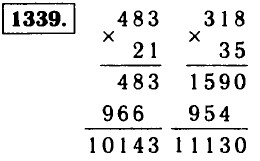
Умножение десятичных дробей на натуральные числа. Домашние работы (окончание)

1322. Между 1 и 3 этажом — 2 пролёта, а между 1 и 9 — восемь, значит лестница на 9 этаж в 8 : 2 = 4 раза длиннее.

1323. а) 7,1 — среднее число равно сумме крайних чисел; б) 0,5 — среднее число равно разности крайних чисел.

1324. а) 2,789 ≈ 2,8; 0,8321 ≈ 0,8; 247,356 ≈ 247,4;
б) 32028,7 ≈ 32 000; 16513,5 ≈ 17000; 811,9 ≈ 1000.

1325. а) 1243,5 + (279,48 + 105,24) = 1243,5 + 384,72 = 1628,22; б) 28,348 - (12,652 - 0,7) = 28,348 - 11,952 = 16,396; в) 542,3 + (600 - 541,3) = 600 + (542,3 - 541,3) = 600 + 1 = 601; г) (38,45 - 27,35) - 8,45 = 38,45 - 8,45 - 27,35 = 30 - 27,35 = 2,65.

1326. а) х + 2,8 - 3,72 + 0,38 ⇒ х = 4,1 - 2,8 = 1,3; б) 4,1 + у - 20,3 - 4,9 ⇒ у = 20,3 - 4,9 - 4,1 = 11,3; в) z - 6,8 = 8,7 + 6,4 ⇒ z = 15,1 + 6,8 = 21,9; г) 10 - υ + 4,3 = 10,7 ⇒ υ = 14,3 - 10,7 = 3,6.

1327. Скорость второго поезда равна (65 + а) км/ч. Скорость удаления поездов друг от друга 65 + (а + 65) = 130 + а км/ч. Через 3 ч между поездами будет (130 + a) • 3 км. При а = 10, (130 + а) = 3 • (130 + 10) = 3 • 140 = 420 км. При а = 25, (130 + а) = (130 + 25) = 155 • 3 = 465 км. При а = 40, (130 + a) • 3 = (130 + 40) • 3 = 170 • 3 = 510 км.

1328. 1) Пусть скорость акулы х км/ч, тогда скорость дельфина 2х км/ч. Скорость дельфина больше скорости акулы на (2х - х) км/ч. Составим и решим уравнение: 2х - х = 25 ⇒ х = 25 км/ч — скорость акулы, а скорость дельфина 2 • 25 = 50 км/ч.
2) Пусть у — масса петуха, тогда масса индюка 5у. Масса петуха меньше массы индюка на (5у - у) кг. Составим и решим уравнение: 5у - у = 8 ⇒ 4у = 8 = 4у = 8 : 4 = 2 кг — масса петуха, а масса индюка равна 5 • 2 = 10 кг.

1329. 1) 5,5 + х - 23,5 = 8,75 ⇒ x = 8,75 + 23,5 - 5,5 = 26,75;
2) 6,2 - у - 1,8 = 4,39 ⇒ у = 4,4 - 4,39 = 0,01.

1330. а) 84,25 • 3 = 252,75; б) 0,255 • 25 = 6,375; в) 0,125 • 312 = 39; г) 6,75 • 144 = 972; д) (4,8 + 3,5) •15 = 8,3 • 15 = 124,5; е) (18,6 - 9,1) • 32 = 9,5 • 32 = 304.

1331. Периметр восьмиугольника 8 • 3,75 = 30 см.

1332. Масса 76 ящиков с яблоками 76 • 30,25 = 2299 кг.

1333. а) 4,55 • 10 = 45,5; б) 18,3 • 10 = 183; в) 0,235 • 10 = 2,35; г) 8,354 • 100 = 835,4; д) 2,3 • 100 = 230; е) 0,048 • 100 = 4,8; ж) 3,8457 • 1000 = 3845,7; з) 0,0358 • 1000 = 35,8; и) 0,003 • 1000 = 3.

1334. а) при х = 8 и у = 6, 15,2х + 1,73у = 15,2 • 8 + 1,73 • 6 = 121,6 + 10,38 = 131,98; при х = 10 и у = 100, 15,2х + 1,73у = 15,2 • 10 + 1,73 • 100 = 152 + 173 = 325; б) при а = 85 и b = 10, 16,52а + 18,1b = 16,52 • 85 + 18,1 • 10 = 1404,2 + 181 = 1585,2.

1335. На поезде Никита проехал больше чем на автобусе на 55,2 • 4 — 40,6 • 3 = 220,8 - 121,8 = 99 км.

1336. Масса всего груза 6 • 0,25 + 3 • 0,44 = 1,5 + 1,32 = 2,82 т.

<<< К началу