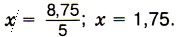|
|
|
|
|
§ 4. Отношения и пропорции 21. ПропорцииОтношения 3,6 : 1,2 и 6,3 : 2,1 равны, так как значения частных равны 3. Поэтому можно записать равенство 3,6 : 1,2 = 6,3 : 2,1, или
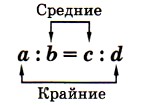
С помощью букв пропорцию записывают так: a : b = с : d или Эти записи читают так: «Отношение а к b равно отношению с к d» или «а так относится к b, как с относится к d». В пропорции
В пропорции
Верно и обратное утверждение:
Это свойство называют основным свойством пропорции. Пропорция 20 : 16 = 5:4 верна, так как 20 • 4 = 16 • 5 = 80. Поменяем местами в этой пропорции средние члены. Получим новую пропорцию: 20 : 5 = 16 : 4. Она тоже верна, так как при такой перестановке произведение крайних и произведение средних членов не изменилось. Эти произведения не изменятся, если в пропорции 20 : 5 = 16 : 4 поменять местами крайние члены. Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны. Используя основное свойство пропорции, можно найти её неизвестный член, если все остальные члены известны. Пример 1. Найдём в пропорции 0,5 : a = 2 : 13 неизвестный средний член а. Р е ш е н и е. Используя основное свойство пропорции, получим а • 2 = = 0,5 • 13. Отсюда Пример 2. Решим уравнение Р е ш е н и е. Используя основное свойство пропорции, получим Что такое пропорция? Как называются числа х и у в пропорции х : а = b : у? Как называются числа m и n в пропорции а : m = n : b? Сформулируйте основное свойство пропорции. Какие перестановки членов пропорции снова приводят к верным пропорциям? Останется ли пропорция верной, если поменять местами какой-нибудь средний её член с одним из крайних? Приведите пример. Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами? Проверьте ваш ответ на пропорции 3:4 = 9: 12.
|
|
|



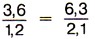
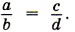
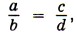 или a : b = с : d, числа a и d называют крайними членами, а числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: а ≠ 0, b ≠ 0, с ≠ 0, d ≠ 0.
или a : b = с : d, числа a и d называют крайними членами, а числа b и с — средними членами пропорции. В дальнейшем будем считать, что все члены пропорции отличны от нуля: а ≠ 0, b ≠ 0, с ≠ 0, d ≠ 0.
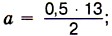 а = 3,25.
а = 3,25.
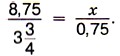
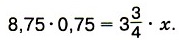 Отсюда
Отсюда 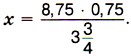 Представим
Представим 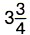 в виде десятичной дроби 3,75 и сократим выражение на 0,75, имеем
в виде десятичной дроби 3,75 и сократим выражение на 0,75, имеем