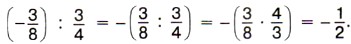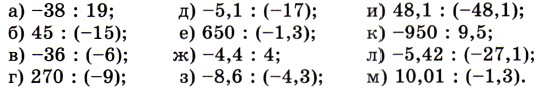36. Деление

Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.

Например, разделить -12 на -4 — это значит найти такое число х, что -4 - х = -12. Сначала найдём знак числа х. Так как при умножении -4 на х получилось отрицательное число -12, то множители -4 и x должны иметь разные знаки. Поэтому х — положительное число. Теперь найдём модуль числа х. Так как модуль произведения равен произведению модулей множителей, то |-12| = |-4| • |х|. Отсюда |х| = |-12| : |-4|. Но так как х — положительное число, то х = |х|. Значит, х = 3.

Пишут: (-12) : (-4) = |-12| : |-4| = 3, или короче:

(-12) : (-4) = 12:4 = 3.

Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.

Например, -4,5 : (-1,5) = 4,5 : 1,5 = 3;

Разделить -24 на 4 — это значит найти такое число х, что 4-х = -24. При умножении 4 на х получилось отрицательное число -24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|х| = |-24|.

Отсюда |х| = |-24| : |4| = 24 : 4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = -6.

Итак, -24 : 4 = -6.

Рассуждая таким же образом, получим, что 24 : (-4) = -6.

При делении чисел с разными знаками, надо:

1) разделить модуль делимого на модуль делителя;

) поставить перед полученным числом знак «-».

Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.

Например, 3,6 : (-3) = -(3,6 : 3) = -1,2;

При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!

Сформулируйте правило деления отрицательного числа на отрицательное.

Сформулируйте правило деления чисел, имеющих разные знаки.

Чему равно частное 0 : а, где а ≠ 0?

1149. Верно ли выполнено деление:

1150. Найдите частное:

Продолжение >>>