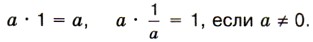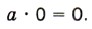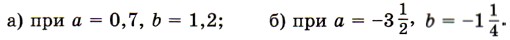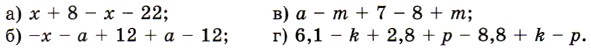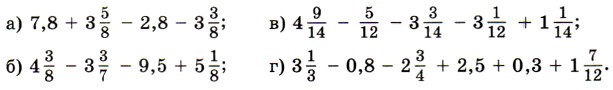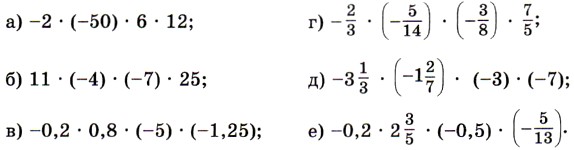38. Свойства действий с рациональными числами

Сложение рациональных чисел обладает переместительным и сочетательным свойствами. Иными словами, если а, b и с — любые рациональные числа, то

Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю. Значит, для любого рационального числа имеем:

Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, если а, b и с — любые рациональные числа, то

Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1. Значит, для любого рационального числа a имеем:

Умножение числа на нуль даёт в произведении нуль, т. е. для любого рационального числа а имеем:

Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если a • b = 0, то либо a = 0, либо b = 0 (может случиться, что и a = 0, и b = 0).

Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел а, b и с имеем:

Перечислите свойства сложения рациональных чисел.

Перечислите свойства умножения рациональных чисел.

В каком случае произведение двух чисел равно нулю?

1201. Сформулируйте словами переместительное свойство сложения а + b = b + а и проверьте его:

1202. Сформулируйте словами сочетательное свойство сложения а + (b + с) = (а + b) + с и проверьте его:

1203. Сложив отдельно положительные и отдельно отрицательные числа, найдите значение выражения:

1204. Сложив сначала противоположные числа, найдите значение выражения:

1205. Упростите выражение:

1206. Выбрав удобный порядок вычислений, найдите значение выражения:

1207. Сформулируйте словами переместительное свойство умножения ab = bа и проверьте его:

1208. Сформулируйте словами сочетательное свойство умножения а(bс) = (ab)c и проверьте его:

1209. Выбирая удобный порядок вычислений, найдите значение выражения:

Продолжение >>>