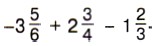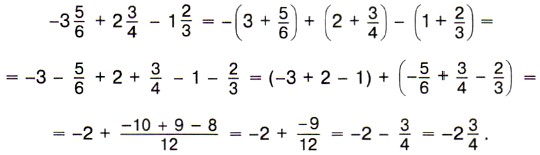39. Раскрытие скобок

Выражение а + (b + с) можно записать без скобок: а + (b + с) = а + b + с. Эту операцию называют раскрытием скобок.

Пример 1. Раскроем скобки в выражении а + (-b + с).

Р е ш е н и е.

а + (-b + с) = а + ((-b) + с) = а + (-b) + с = а - b + с.

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

Пример 2. Найдём значение выражения

-2,87 + (2,87 - 7,639).

Р е ш е н и е. Раскрывая скобки, получим

-2,87 + (2,87 - 7,639) = -2,87 + 2,87 - 7,639 = 0 - 7,639 = -7,639.

Чтобы найти значение выражения -(-9 + 5), надо сложить числа -9 и 5 и найти число, противоположное полученной сумме: -(-9 + 5) = -(-4) = 4.

То же значение можно получить по-другому: вначале записать числа, противоположные данным слагаемым (т. е. изменить их знаки), а потом сложить: 9 + (-5) = 4. Таким образом,

-(-9 + 5) = 9 - 5 = 4.

Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.

Значит, -(а + b) = -а - b.

Пример 3. Найдём значение выражения

16 - (10 - 18 + 12).

Р е ш е н и е.

16 - (10 - 18 + 12) = 16 + (-(10 - 18 + 12)) =
= 16 + (-10 + 18 - 12) = 16 - 10 + 18 - 12 = 12.

Чтобы раскрыть скобки, перед которыми стоит знак «-», надо заменить этот знак на «+», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

Пример 4. Найдём значение выражения

9,36 - (9,36 - 5,48).

Р е ш е н и е.

9,36 - (9,36 - 5,48) = 9,36 + (-9,36 + 5,48) =
= 9,36 - 9,36 + 5,48 = 0 + 5,48 = 5,48.

Раскрытие скобок и применение переместительного и сочетательного свойств сложения позволяют упрощать вычисления.

Пример 5. Найдём значение выражения

(-4 - 20) + (6 + 13) - (7 - 8) - 5.

Р е ш е н и е. Сначала раскроем скобки, потом найдём отдельно сумму всех положительных и отдельно сумму всех отрицательных чисел и, наконец, сложим полученные результаты:

(-4 - 20) + (6 + 13) - (7 - 8) - 5 = -4 - 20 + 6 + 13 - 7 + 8 - 5 =
= (6 + 13 + 8) + (-4 - 20 - 7 - 5) = 27 - 36 = -9.

Пример 6. Найдём значение выражения

Р е ш е н и е. Сначала представим каждое слагаемое в виде суммы их целой и дробной частей, затем раскроем скобки, потом сложим отдельно целые и отдельно дробные части и, наконец, сложим полученные результаты:

Продолжение >>>