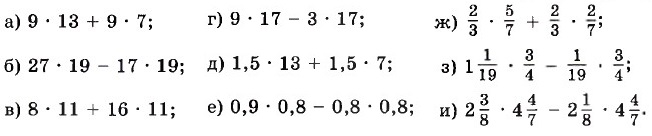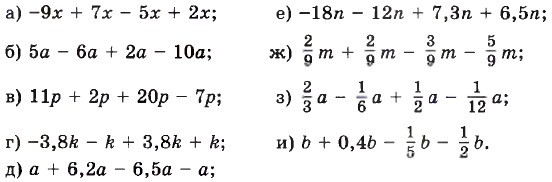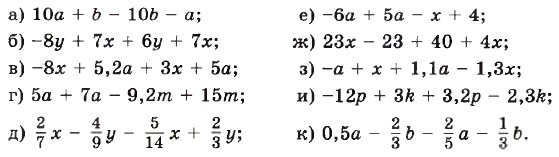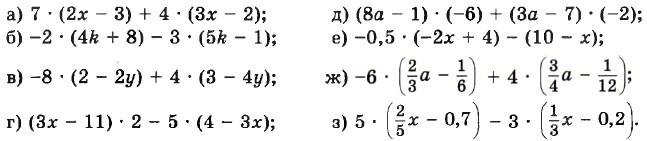41. Подобные слагаемые

Распределительное свойство умножения (а + b) • с = ас + bс справедливо для любых чисел а, b и с.

Замену выражения (а + b) • с выражением ас + bс или выражения с • (а + b) выражением са + сb также называют раскрытием скобок.

Пример 1. Раскроем скобки в выражении -3 • (а - 2b).

Р е ш е н и е. Умножим -3 на каждое из слагаемых а и -2b. Получим -3 • (а - 2b) — -3 • а + (-3) • (-2b) = -За + 6b.

Пример 2. Упростим выражение 2m - 1m + 3m.

Р е ш е н и е. В данном выражении все слагаемые имеют общий множитель m. Значит, по распределительному свойству умножения 2m - 1m + 3m = m • (2 - 7 + 3). В скобках записана сумма коэффициентов всех слагаемых. Она равна -2. Поэтому 2m - 1m + 3m = -2m.

В выражении 2m - 1m + 3m все слагаемые имеют общую буквенную часть и отличаются друг от друга только коэффициентами. Такие слагаемые называют подобными.

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Подобные слагаемые могут отличаться только коэффициентами.

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Пример 3. Приведём подобные слагаемые в выражении 5а + а - 2а.

Р е ш е н и е. В данной сумме все слагаемые подобны, так как у них одинаковая буквенная часть а. Сложим коэффициенты: 5 + 1 - 2 = 4. Значит, 5а + а - 2а = 4а.

Какие слагаемые называют подобными?

Чем могут отличаться друг от друга подобные слагаемые?

На основании какого свойства умножения выполняют приведение (сложение) подобных слагаемых?

1281. Раскройте скобки:

1282. Выполните действия, применив распределительное свойство умножения:

1283. Сложите подобные слагаемые:

1284. Выполните приведение подобных слагаемых:

1285. Раскройте скобки и приведите подобные слагаемые:

1286. Найдите значение выражения:

Продолжение >>>