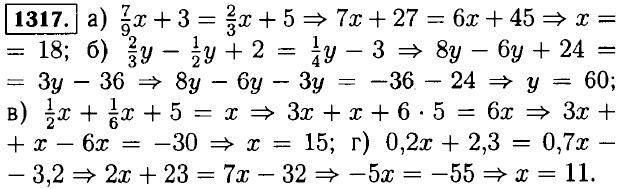Решение уравнений. Домашние работы

1314. а) 8х + 5,9 = 7х + 20 ⇒ 8х = 7х + 20 - 5,9; б) 6х - 8 = -5х - 1,6 ⇒ 6х = -5х - 1,6 + 8.

1315. а) 15у - 8 = -6у + 4,6 ⇒ 15у + 6у = 4,6 + 8; б) -16z + 1,7 = 2z - 1 ⇒ -16z - 2z = -1 - 1,7.

1316. а) 6х - 12 = 5х + 4 ⇒ 6х - 5х = 4 + 12 ⇒ х = 16; б) -9а + 8 = -10а - 2 ⇒ -9а + 10а = -2 - 8 ⇒ а = -10; в) 7m + 1 = 8m + 9 ⇒ 7m - 8m = 9 - 1 ⇒ m = -8; г) -12n - 3 = 11n - 3 ⇒ -12n - 11n = -3 + 3 ⇒ -23n = 0 ⇒ n = 0; д) 4 + 25у = 6 + 24у ⇒ 25у - 24у = 6 - 4 ⇒ у - 2; е) 11 - 5z = 12 - 6z ⇒ -5z + 6z = 12 - 11 ⇒ z = 1; ж) 4k + 7 = -3 + 5k ⇒ 4k - 5k = -3 - 7 ⇒ k = 10; з) 6 - 2с = 8 - Зс ⇒ -2с + 3с = 8 - 6 ⇒ с = 2.

1318. а) -40 • (-7х + 5) = -1600 ⇒ 280x - 200 = -1600 ⇒ 280х = -1400 ⇒ х = -5. Проверка: -40 • (-7 • (-5) + 5) = -1600 ⇒ -40 • 40 = -1600 ⇒ -1600 = -1600; б) (-20x - 50) • 2 = 100 ⇒ -40x - 100 = 100 ⇒ -40x - 200 ⇒ х = -5. Проверка: (-20 • (-5) - 50) • 2 - 100 ⇒ (100 - 50) • 2 = 100 ⇒ 100 = 100; в) 2,1 • (4 - 6у) = -42 ⇒ 8,4 - 12,6у = -42 ⇒ -12,6у = -50,4 ⇒ у = 4. Проверка: 2,1 • (4 - 6 • 4) = -42 ⇒ 2,1 • (-20) = -42 ⇒ -42 = -42; г) -3 • (2 - 15x) = -6 ⇒ -6 + 45х = -6 ⇒ 45х = 0 ⇒ х = 0. Проверка: -3 • (2 - 15 • 0) = -6 ⇒ -3 • 2 = -6 ⇒ -6 = -6.

1322. Пусть х — длина отрезка АВ, тогда длина отрезка CD равна х — 2 см. Если длину отрезка АВ увеличить на 10 см, а длину отрезка CD увеличить в 3 раза, то получатся равные результаты. Составим и решим уравнение: х + 10 = 3(х - 2) х + 10 = 3х - 6 ⇒ -2х = -16 ⇒ х = 8 см.

1323. Пусть х — скорость автобуса, тогда скорость легковой автомашины будет рана х + 50 км/ч. Одно и то же расстояние от города до села автобус проходит за 1,8 ч, а легковая машина за 0,8 ч. Составим и решим уравнение: 1,8x = (х + 50) • 0,8 ⇒ 1,8x - 0,8x = 40 ⇒ х = 40 км/ч.

1324. Пусть на первую автомашину погрузили х т зерна, тогда на вторую х - 0,6 т. Если бы на первую автомашину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих машинах было бы поровну. Составим и решим уравнение: 1,2x = 1,4(x - 0,6) ⇒ 1,2x - 1,4x = -0,84 ⇒ 0,2x = 0,84 ⇒ х = 4,2 т погрузили на первую автомашину. На вторую автомашину погрузили: х - 0,6 = 4,2 - 0,6 = 3,6 т.

1328. Пусть х — длина первого куска верёвки, тогда 63 - х м длина второго куска. 0,4 длины первого куска равно 0,3 длины второго куска. Составим и решим уравнение: 0,4x = 0,3 ⇒ (63- x) ⇒ 0,4x + 0,3x = 18,9 ⇒ х = 27 м — длина первого куска, а длинна второго куска: 63 - х = 63 - 27 = 36 м.

1330. Пусть в растворе было х г соли, тогда масса всего раствора была равна: х : 0,4 = 2,5x г. После того, как в раствор добавили 120 г соли, в растворе стало x + 120 г соли, а масса раствора стала равняться 2,5x + 120 г. В растворе стало содержаться 70% соли. Составим и решим уравнение: (2,5x + 120) ⇒ 0,7 = х + 120 ⇒ 1,75x + 84 = х + 120 ⇒ 0,75x = 36 ⇒ х = 48 г.

1331. а) -62, -81, -27, 54; б) 81, -27, -40, -34; в) -64, -4, -81, 27; г) -90, -10, 130, -130.

<<< К началу Решенния (окончание) >>>