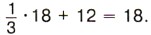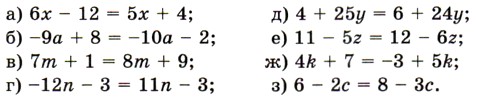|
|
|
|
|
§ 8. Решение уравнений 42. Решение уравненийПример 1. Решим уравнение 4 • (х + 5) = 12. Р е ш е н и е. По правилу отыскания неизвестного множителя имеем х + 5 = 12 : 4, т. е. х + 5 = 3. Это же уравнение можно получить, разделив обе части данного уравнения на 4 или умножив обе части на Число -2 является корнем уравнения х + 5 = 3 и уравнения 4 • [х + 5) = 12, так как -2 + 5 = 3 и 4 • (-2 + 5) = 12.
Пример 2. Решим уравнение 2х + 5 = 17. Р е ш е н и е. По правилу отыскания неизвестного слагаемого имеем 2х = 17 - 5, т. е. 2х = 12. Уравнения 2х + 5 = 17 и 2x = 17 - 5 имеют один и тот же корень 6, так как 2 • 6 + 5=17 и 2 • 6=17 - 5. Уравнение 2х = 17 - 5 можно записать так: 2х = 17 + (-5). Видим, что корень уравнения 2х + 5 = 17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.
Пример 3. Решим уравнение 5x = 2x + 6 (рис. 93). Р е ш е н и е. Вычтем из обеих частей уравнения по 2х (снимем с обеих чашек весов по две буханки хлеба). Получим 5x - 2х = 2х - 2х + 6. Но 2х - 2х = 0, значит, 5x - 2x = 6. Это уравнение можно получить из данного, если слагаемое 2x перенести из правой части в левую, изменив его знак на противоположный. Решая дальше уравнение 5х - 2х = 6, получим 3x = 6 и х = 2. Число 2 есть корень уравнения 5x - 2х = 6 и уравнения 5x = 2x + 6, так как 5 • 2 - 2 • 2 = 6 и 5 • 2 = 2 • 2 + 6.
Пример 4. Решим уравнение Р е ш е н и е. Умножим левую и правую части уравнения на 3 для того, чтобы освободиться от дробного коэффициента. Получим х + 36 = Зx. Перенесём с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое Зx из правой части в левую: x - Зx = -36. Упростим левую часть уравнения: -2x = -36. Теперь разделим обе части уравнения на -2, получим x = 18. Число 18 является корнем данного уравнения Во всех рассмотренных примерах мы приводили данные уравнения к виду ах = b, где а ≠ 0. Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным. Обе части уравнения умножили на число, не равное 0. Изменились ли корни данного уравнения? Обе части уравнения разделили на одно и то же число, отличное от нуля. Изменились ли корни данного уравнения? Сформулируйте правило переноса слагаемых из одной части уравнения в другую. Какие уравнения называют линейными? 1314. Перенесите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:
1315. Соберите в левой части уравнения все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное:
1316. Решите уравнение:
1317. С помощью умножения обеих частей уравнения на одно и то же число освободитесь от дробных чисел и решите уравнение:
|
|
|



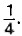 Теперь легко найти значение х. Имеем х = 3 - 5, или х = -2.
Теперь легко найти значение х. Имеем х = 3 - 5, или х = -2.

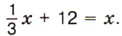
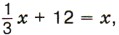 так как верно
равенство
так как верно
равенство