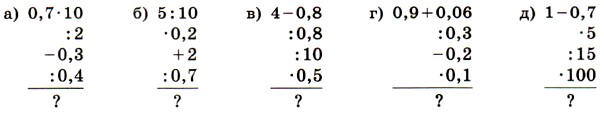6. Наибольший общий делитель. Взаимно простые числа (продолжение)

146. Найдите все общие делители чисел:

а) 18 и 60;
б) 72, 96 и 120;
в) 35 и 88.

147. Найдите разложение на простые множители наибольшего общего делителя чисел а и b, если:

а) а = 2 • 2 • 3 • 3 и b = 2 • 3 • 3 • 5;
б) а = 5 • 5 • 7 • 7 • 7 и b = 3 • 5 • 7 • 7.

148. Найдите наибольший общий делитель чисел:

а) 12 и 18;
б) 50 и 175;
в) 675 и 825;
г) 7920 и 594;
д) 324, 111 и 432;
е) 320, 640 и 960.

149. Являются ли взаимно простыми числа:

а) 35 и 40;
б) 77 и 20;
в) 10, 30, 41;
г) 231 и 280?

150. Найдите среди чисел 9, 14, 15 и 27 три пары взаимно простых чисел.

151. Запишите все правильные дроби со знаменателем 12, у которых числитель и знаменатель — взаимно простые числа.

152. Ребята получили на новогодней ёлке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на ёлке? Сколько апельсинов и сколько яблок было в каждом подарке?

153. Для поездки за город работникам завода было выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. В лес поехали 424 человека, а на озеро — 477 человек. Все места в автобусах были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе?

154. Вычислите устно:

155. С помощью рисунка 7 определите, являются ли числа a, b и с простыми.

156. Существует ли куб, ребро которого выражается натуральным числом и у которого:

а) сумма длин всех рёбер выражается простым числом;
б) площадь поверхности выражается простым числом?

157. Разложите на простые множители числа:

а) 875; 2376; 5625;
б) 2025; 3969; 13 125.

158. Почему, если одно число можно разложить на два простых множителя, а другое — на три простых множителя, то эти числа не равны?

159. Можно ли найти четыре различных простых числа, чтобы произведение двух из них равнялось произведению двух других?

160. Сколькими способами в девятиместном микроавтобусе могут разместиться 9 пассажиров? Сколькими способами могут разместиться пассажиры, если один из них, хорошо знающий маршрут, сядет рядом с водителем?

<<< К началу Окончание >>>