|
|
|
|
|
§ 9. Координаты на плоскости
48. Вопросы и задачи на повторение (продолжение)1500. Площадь прямоугольника равна 12 см2. Длины сторон прямоугольника равны а см и b см. Найдите а, если b = 2; 4; 6; 12. Найдите формулу зависимости а от b. Является ли эта зависимость обратно пропорциональной? 1501. Решите уравнение:
1502. За 1503. Масса муки составляет 0,7 массы выпеченного из неё хлеба. Сколько получится хлеба, если взять 1504. Начертите окружность, радиус которой 2,5 см, и отрезок, длина которого равна длине окружности (длину окружности округлите до десятых долей сантиметра). 1505. Сравните площадь круга, радиус которого 6 см, и площадь прямоугольника со сторонами 6,5 см и 1,4 дм. 1506. Назовите коэффициент выражения:
1507. Сформулируйте правило приведения подобных слагаемых. 1508. Какие правила необходимо применять для решения уравнения:
1509. Выполните действия:
1510. При х = 2; -2;
1511. Упростите выражение. Найдите его значение при
1512. Решите уравнение:
1513. Газовая туристская плитка и два баллона имеют массу 7 кг. Масса плитки меньше массы баллона на 2 кг. Найдите массу баллона. 1514. Кофейник и две чашки вмещают 740 г воды. В кофейник входит на 380 г воды больше, чем в чашку. Сколько граммов воды вмещает кофейник? 1515. За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг меньше, чем в первый, а в третий — в 3 раза больше, чем во второй. Сколько килограммов апельсинов было продано в первый день? 1516. Велосипедист проехал 43 км. По просёлочной дороге он проехал в 3 раза большее расстояние, чем по лесной тропинке, а по тропинке на 35 км меньше, чем по шоссе. Какой длины была каждая часть пути? 1517. Решите уравнение:
1518. Площадь двух участков, засеянных кукурузой, равна 60 га. На одном участке с каждого гектара собрали 85 т зелёной массы, а на другом — 95 т. С первого участка собрали на 1500 т больше, чем со второго. Найдите площадь каждого участка. 1519. В одной силосной яме 110 т силоса, а в другой — 130 т. После того как из второй ямы взяли силоса в 2 раза больше, чем из первой, в первой оказалось на 5 т больше, чем во второй. Сколько тонн силоса взяли из каждой ямы? 1520. Периметр треугольника АВС равен 85 см. Сторона АВ меньше стороны ВС на 15 см, а сторона АС больше стороны АВ на 22 см. Найдите длину стороны ВС. 1521. Сумма четырёх последовательных целых чисел равна 2. Найдите эти числа. 1522. Сумма пяти последовательных целых чисел равна -10. Найдите эти числа. 1523. В летние каникулы я проехал на поезде на 120 км больше, чем проплыл на теплоходе. Если бы я проехал на поезде в 4 раза больше, а на теплоходе проплыл в 8 раз больше, чем в действительности, то общий путь составил бы 1200 км. Сколько километров я проплыл на теплоходе? 1524. Как найти: а) дробь от числа; б) число по его дроби; в) масштаб карты; г) расстояние на местности по известному расстоянию на карте и масштабу карты? 1525. Длина дороги 25,5 км. За 5 дней бригада отремонтировала 1526. Решите двумя способами задачу: а) В районе зерновыми культурами занято 52,5 км2. Рожь занимает
б) Собрали 72,8 т фруктов. Половину этих фруктов отправили в магазины, четверть — в школы и детские сады, а остальные заложили на хранение поровну в 4 холодильника. Сколько тонн фруктов заложили в каждый холодильник? 1527. В школе учатся 360 девочек. Сколько учащихся в школе, если мальчики составляют 52 % всех учащихся? 1528. Фермер снял с каждого из 9 га своей плантации 35 т овощей. Консервный завод купил 12% собранных фермером овощей. Сколько тонн овощей купил консервный завод у фермера? 1529. Для строительства железной дороги будет поставляться 70 тыс. т проката, из которых 50 тыс. т — прокат, устойчивый при низких температурах. Какой процент всего проката составит прокат, устойчивый при низких температурах? 1530. Жильцы дома решили озеленить свой двор. Они разбили газон площадью 250 м2. На каждые 100 м2 они высевали 1,2 кг смеси семян. В эту смесь входило: 1531. Сколькими числами определяется положение точки: а) на координатной прямой; б) на координатной плоскости? Как называют эти числа? 1532. Постройте точки: а) на координатной прямой: М(-3), 1533. На координатной плоскости постройте треугольник АВС, если А(-3; 6), В(-3; -4), С(2; -4). Запишите координаты точек пересечения сторон треугольника с осями координат. 1534. На координатной плоскости начертите треугольник МКР, если М(-5; 5), К(-4; 9), Р(5; 10). Измерьте транспортиром углы этого треугольника. 1535. Постройте квадрат ABCD по координатам его вершин А(0; 3), В(3; 6), С(6; 3) и D(3; 0). Проведите отрезки АС и BD. Найдите координаты точки, в которой пересекаются эти отрезки. 1536. На координатной плоскости начертите окружность с центром в точке С(-4; 0) и радиусом, равным 5 единичным отрезкам. Запишите координаты точек пересечения окружности с осями координат. 1537. Отметьте на координатной плоскости вершины А(-4; 2), В(1; 7) и С(6; 2) квадрата ABCD. Найдите координаты вершины D. 1538. Турист шёл в гору со скоростью 3 км/ч. Пройденный им путь можно вычислить по формуле s = 3t. Является ли зависимость пути, пройденного туристом, от времени прямой или обратной пропорциональной зависимостью? Составьте таблицу значений s для t = 1; 2; 3; 4; 5 ч. Постройте график движения туриста. 1539. Сумма двух чисел — 177. При делении большего из них на меньшее в частном получается 3 и в остатке 9. Найдите эти числа. 1540. От причала вниз по реке отправили плот, который двигался со скоростью 4 км/ч. Через 3 ч вслед за ним вышла лодка. Её собственная скорость 9 км/ч. На каком расстоянии от причала лодка догонит плот? 1541. Велосипедист и пешеход одновременно отправились навстречу ДРУГ другу из двух пунктов, расстояние между которыми 6,2 км. При встрече оказалось, что пройденный пешеходом путь составляет 1542. Расстояние между городами А и В равно 450 км. Из А в В вышла грузовая автомашина. Спустя 2 ч навстречу ей из В вышла легковая автомашина. Скорость грузовой автомашины 60 км/ч, а скорость легковой в 1543. Какие прямые называют перпендикулярными? Какие отрезки считают перпендикулярными? Постройте такие отрезки. Какие лучи считают перпендикулярными? Постройте такие лучи. 1544. Какие прямые называют параллельными? Какие отрезки считают параллельными? Постройте три параллельные прямые. 1545. Начертите угол CDK, равный 130°. Отметьте точку М, не лежащую на сторонах этого угла, и проведите через точку М прямые, параллельные сторонам угла CDK. 1546. Начертите угол AJPK, равный 80°. Отметьте на стороне РА точку М и проведите через неё прямые, перпендикулярные сторонам угла АРК. 1547. На координатной плоскости отметьте точки А(-5; 10), В(3; -6), С(-3; -4), D(9; 2), Е(-7; 4), F(3; 9), К(4; 5), Р(7; 14), М(-8; -4) и N(-6; 2). Проведите прямые АВ, CD, EF, КР и MN. С помощью чертёжного угольника и линейки определите, какие из этих прямых параллельны и какие перпендикулярны друг другу. Определите координаты точки пересечения прямой CD с осью х и координаты точки пересечения прямой КР с осью у. 1548. Лесорубы заготовили 32000 м3 строительного леса. По реке сплавили 60 % заготовленного леса, а остальной отправили по железной дороге. На сколько кубометров меньше леса отправили по железной дороге, чем по воде? 1549. На ремонт физкультурного зала было израсходовано 44 кг краски, что составляет 20% всей краски, отпущенной со склада на ремонт школы. Сколько килограммов краски было на складе, если школе отпущено 12,5% имевшейся там краски?
|
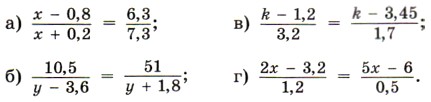
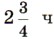поезд прошёл расстояние 330 км. Какой путь пройдёт 4 поезд за 7,5 ч, если будет идти с той же скоростью?
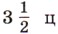муки? Сколько муки надо взять, чтобы выпечь 100 кг хлеба?
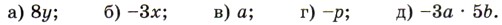
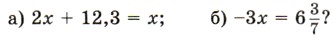
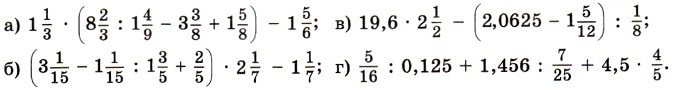
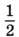найдите значение выражения:
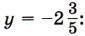
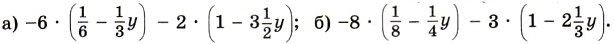
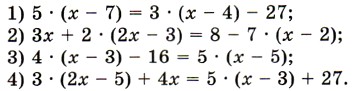
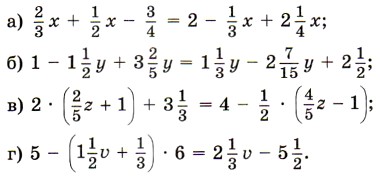
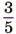дороги, ремонтируя ежедневно участки дороги одинаковой длины. Сколько километров дороги бригада ремонтировала за один день?
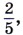а пшеница — 
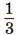всех посевов. Остальную часть занимает ячмень. Сколько гектаров занимает ячмень?
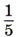мятлика лугового, 
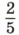овсяницы и 40% райграса пастбищного. Сколько семян каждого вида понадобилось?
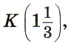Р(-0,6); б) на координатной плоскости: В(-1; 4), С(0; 5), D(-2; 0). В упражнении б) назовите абсциссу и ординату каждой точки.
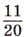пути, проделанного велосипедистом. Сколько часов был в пути велосипедист до встречи с пешеходом, если его скорость была на 4,5 км/ч больше скорости пешехода?
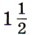раза больше. Постройте графики движения обеих автомашин. Через сколько часов после своего выхода легковая автомашина встретит грузовую?
|
|