|
|
|
|
|
Глава 1. Электростатика Напряженность электрического поля. Принцип суперпозиции полейНапряженность поля точечного заряда
Найдем напряженность поля, создаваемого точечным зарядом q. Этот заряд действует на другой заряд q0 с силой, согласно закону Кулона равной:
где Напряженность поля точечного заряда q на расстоянии r от него равна:
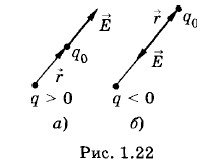
Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд, — от заряда, если q > 0 (см. рис. 1.22, а), и к заряду, если q < 0 (см. рис. 1.22, б). Принцип суперпозиции полейЕсли на тело действует несколько сил, то по законам механики Ньютона результирующая сила равна геометрической сумме сил:
В интересующем нас случае телом является заряженное тело или, говоря коротко, электрический заряд. На электрические заряды действуют силы со стороны поля. Если при наложении в пространстве полей от нескольких зарядов эти поля не оказывают никакого влияния друг на друга, то результирующая сила со стороны всех полей должна быть равна геометрической сумме сил со стороны каждого поля. Именно так и происходит на самом деле. Это означает, что напряженности полей складываются геометрически, так как напряженности прямо пропорциональны силам. В этом состоит принцип суперпозиции полей, т. е. принцип независимого наложения полей («суперпозиция» в переводе на русский означает «наложение»). Он формулируется так: если в данной точке пространства различные заряды создают электрические поля, напряженности которых
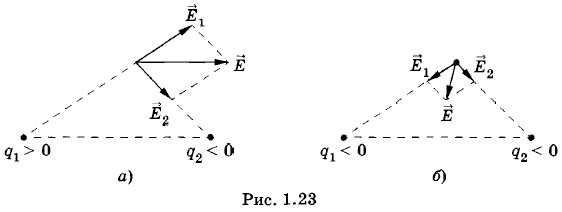
Благодаря принципу суперпозиции для нахождения напряженности поля системы точечных зарядов в любой точке достаточно знать выражение (1.9.5) для напряженности поля точечного заряда. На рисунке 1.23, а, б показано, как геометрически определяется напряженность Е поля, созданного двумя зарядами.
Для определения напряженности поля, создаваемого заряженным телом конечных размеров, нужно поступать следующим образом. Мысленно разделить тело на маленькие элементы, каждый из которых можно считать точечным. Определить заряды всех этих элементов и найти напряженности полей, созданных всеми ими в заданной точке. После этого сложить геометрически напряженности от всех элементов тела и найти результирующую напряженность поля. Для тел сложной формы это трудная, но в принципе разрешимая задача. Для ее решения нужно знать, как заряд распределен на теле. Подчеркнем, что принцип суперпозиции не является тривиальным. Поля, удовлетворяющие этому принципу, называются линейными*. * Поля являются линейными, если уравнения, описывающие их эволюцию или распределение в пространстве, линейны, т. е. не содержат квадратов и более высоких степеней рассматриваемых величин. У линейных полей отсутствуют взаимодействия между отдельными участками поля: поле не действует само на себя. Электромагнитное поле линейно. Но гравитационное поле в теории тяготения Эйнштейна является нелинейным. Нелинейно также поле, осуществляющее сильные взаимодействия между кварками.
|
|
|




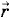 — радиус-вектор, проведенный от заряда q к заряду q0 (рис. 1.22, а, б).
— радиус-вектор, проведенный от заряда q к заряду q0 (рис. 1.22, а, б).

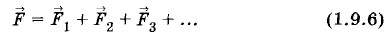
 1,
1,