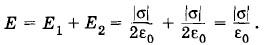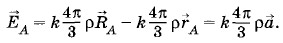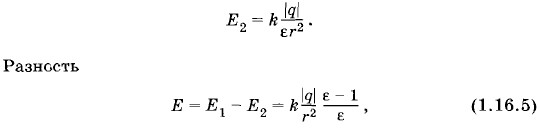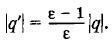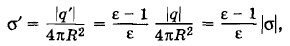|
|
|
|
|
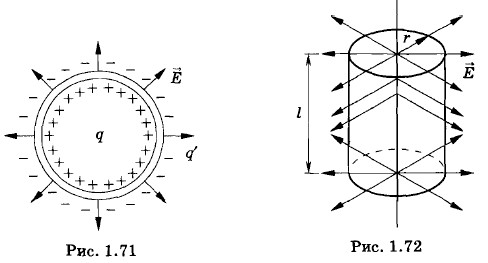
Глава 1. Электростатика Примеры решения задачЗадача 4На расстоянии d от большой проводящей пластины находится точечный электрический заряд +q. С какой силой действует на него пластина? Решение. Под влиянием заряда +q на пластине появляются наведенные отрицательные заряды. Они распределяются по поверхности пластины таким образом, что результирующая напряженность электрического поля, созданного этими зарядами и зарядом +q, внутри пластины равна нулю (индуцированные положительные заряды уходят на удаленные края пластины, и их влиянием можно пренебречь). Поскольку плас тина большая, модуль суммарного наведенного заряда равен q. Справа от пластины (рис. 1.67) электрическое поле создается точечным зарядом + q и распределенным по поверхности пластины наведенным отрицательным зарядом -q. Слева электрическое поле отсутствует (эффект электростатической защиты).
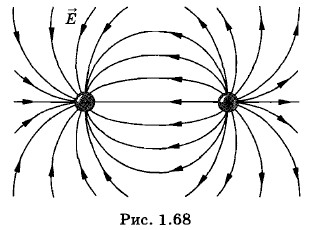
Представим себе, что мы поместили слева от пластины на расстоянии d точечный отрицательный заряд —q (заряд-изображение). Он наведет на левой поверхности пластины положительные заряды, которые распределятся по ней точно так же, как отрицательные заряды на правой поверхности. При этом электрическое поле справа от пластины не изменится (опять действует электростатическая защита). Можно сказать, что справа от пластины поле создается двумя точечными зарядами +д и —q и зарядами (отрицательными и положительными), индуцированными на обеих сторонах пластины. (Ведь суммарная напряженность электрического поля от точечного отрицательного заряда и наведенных положительных зарядов справа от пластины равна нулю.) Если пластина тонкая (ее толщина мала по сравнению с расстоянием d), то напряженность поля наведенных зарядов вне пластины равна нулю. Таким образом, оказывается, что справа от пластины электрическое поле, создаваемое зарядом +q и наведенными отрицательными зарядами, совпадает с полем, созданным двумя точечными зарядами +q и -q, находящимися на расстоянии 2d друг от друга (рис. 1.68). Это означает, что напряженность поля индуцированных зарядов в точке, где находится заряд +q, равна напряженности поля точечного заряда -q. Тогда для искомой силы притяжения получим:
Задача 5Найдите напряженность электрического поля вблизи участка поверхности проводника с известной поверхностной плотностью электрического заряда σ. Решение. Очень близко к заряженной поверхности напряженность электрического поля (в СИ) определяется по формуле (ε = 1)
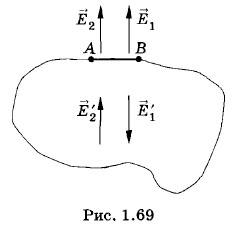
так как очень малый участок поверхности АВ (рис. 1.69) можно считать плоским, и вблизи этого участка справедлива формула (1.12.5) для напряженности поля равномерно заряженной плоскости. Это поле создается по обе стороны заряженной поверхности:
Задача 6Внутри заряженного шара с постоянной объемной плотностью электрического заряда ρ имеется сферическая полость. Расстояние между центрами шара и полости равно а. Найдите напряженность
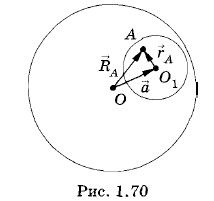
Решение. Заряженный шар с полостью эквивалентен шару, равномерно заряженному по всему объему, внутри которого имеется сфера с зарядом противоположного знака и той же по модулю объемной плотностью заряда ρ. Тогда суммарный заряд этой части шара равен нулю, что соответствует наличию полости в шаре. Напряженность поля в произвольной точке А полости равна векторной сумме напряженностей поля, созданного сплошным заряженным шаром, и поля, созданного шаром, занимающим сферическую полость (рис. 1.70):
Как видно из полученного результата, напряженность поля в полости не зависит от положения выбранной точки А. Она во всех точках одинакова и направлена параллельно прямой, соединяющей центр шара и центр полости; поле однородно. Задача 7Металлический шар радиусом R, имеющий заряд q, находится внутри диэлектрика с диэлектрической проницаемостью ε. Определите поляризационный заряд, возникающий в диэлектрике у поверхности заряженного шара, и поверхностную плотность поляризационного заряда. Решение. Если бы вокруг шара не было диэлектрика, то он создавал бы в окружающем пространстве поле с напряженностью
При наличии диэлектрика возникает поле с напряженностью
очевидно, равна напряженности поля, которое создает поверхностный поляризационный заряд q', появляющийся возле заряженного шара (рис. 1.71). Заряд q' противоположен по знаку заряду q. Так как поляризационный заряд распределен равномерно по поверхности сферы, то
Сопоставляя выражения (1.16.5) и (1.16.6) для Е, найдем:
Поверхностная плотность поляризационных зарядов равна
где σ — поверхностная плотность заряда q на шаре. Задача 8Найдите напряженность электрического поля, создаваемого в вакууме бесконечно длинной заряженной нитью с линейной плотностью заряда τ. Решение. Проще всего решить задачу с помощью теоремы Гаусса. Вычислим поток напряженности через цилиндр, ось которого совпадает с заряженной нитью (рис. 1.72). Радиус цилиндра r, атего высота l. Из соображений симметрии очевидно, что линии напряженности N = 2πrlЕn. (1.16.7) Поток через основания равен нулю. Внутри цилиндра находится заряд q = τl.
Согласно теореме Гаусса, записанной в абсолютной системе единиц, 2πrlЕn = 4πτl. (1.16.8) Отсюда модуль напряженности поля равен:
|
|
|



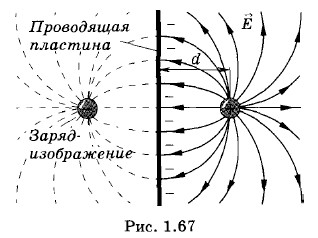
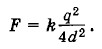
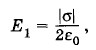
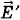 1 = -
1 = - 1. Кроме того, вблизи данного элемента поверхности зарядами, расположенными на всей остальной поверхности проводника, создается поле напряженностью
1. Кроме того, вблизи данного элемента поверхности зарядами, расположенными на всей остальной поверхности проводника, создается поле напряженностью