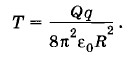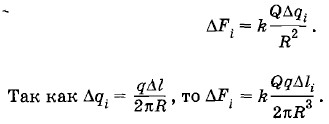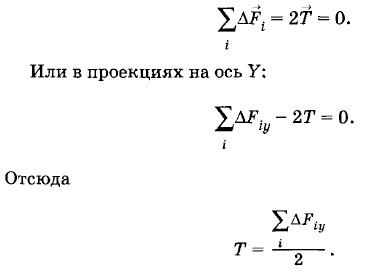|
|
|
|
|
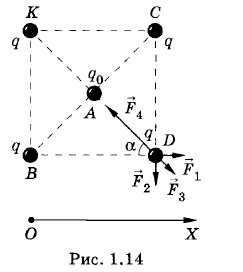
Глава 1. Электростатика § 1.6. Примеры решения задач (окончание)Задача 4В вершинах квадрата расположены одинаковые заряды q. Какой заряд q0 надо поместить в центре квадрата, чтобы система находилась в равновесии?
Решение. Искомый заряд q0 должен к притягивать заряды q, расположенные в вершинах квадрата, компенсируя их взаимное отталкивание. Поэтому знаки зарядов q0 и q противоположны. При любом значении заряда q0 он будет находиться в равновесии, так как расположен в центре симметрии квадрата, и силы, действующие на него со стороны зарядов, расположенных в вершинах квадрата, компенсируются. Заряды, расположенные в вершинах квадрата, будут находиться в равновесии, когда суммы действующих на них сил равны нулю. Рассмотрим, например, условие равновесия заряда, расположенного в точке D (рис. 1.14). На этот заряд действуют силы отталкивания
В проекциях на ось X это равенство примет вид: F4 + F3cos α - F4cos α = 0, (1.6.2) где α = 45 , a Для нахождения модулей сил необходимо знать расстояния между зарядами. Обозначим длину стороны BD квадрата через а, тогда
Подставляя эти силы в уравнение (1.6.2), получим:
Учитывая, что заряды q и q0 должны иметь противоположные знаки, получим:
Задача 5Тонкое проволочное кольцо радиусом Д несет электрический заряд q. В центре кольца расположен одноименный с q заряд Q, причем Q » q. Определите силу, растягивающую кольцо. Решение. 1-й способ. Так как Q » q, то взаимодействием между отдельными элементами кольца можно пренебречь. Выделим малый элемент кольца длиной Δl = RΔα (рис. 1.15, о). Со стороны заряда Q на него действует сила
Силы натяжения
Подставляя в (1.8.3) значения
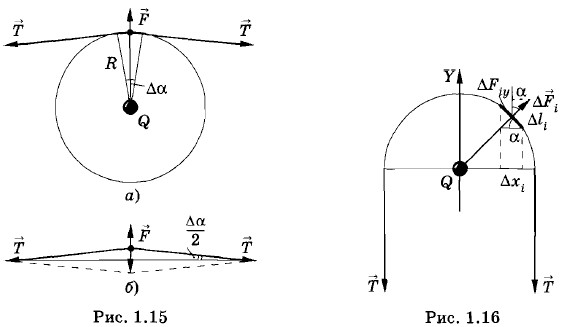
2-й способ. На каждый элемент кольца длиной Alt (рис. 1.16) действует элементарная сила
Геометрическая сумма элементарных сил, действующих на полукольцо, уравновешивается возникающими силами натяжения кольца (см. рис. 1.16):
|
|
|



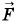 1,
1, 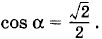
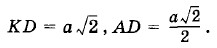

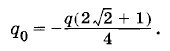
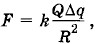 где
где
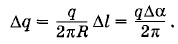
 уравновешивают силу
уравновешивают силу 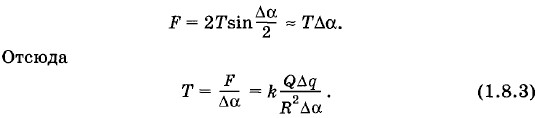
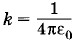 и
и 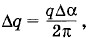 получим:
получим: