|
|
|
|
|
Глава 4. Магнитное поле токов Закон Био—Савара—ЛапласаВекторное произведениеЗакон Био—Савара—Лапласа можно записать в векторной форме, используя понятие векторного произведения двух векторов. Это понятие у нас еще не встречалось. В физике многие величины выражаются через векторные произведения. Векторное произведение используется не менее часто, чем скалярное, о котором шла речь в «Механике» (см. § 6.2). Для обозначения векторного произведения двух векторов Модуль с векторного произведения векторов
Направление векторного произведения задается правилом правого буравчика (или винта). Если рукоятку буравчика поворачивать на наименьший угол от вектора Конечно, нужно еще доказать, что направленный отрезок Отметим лишь, что векторное произведение некоммутативно:
Это следует из определения направления векторного произведения.
Закон Био—Савара—Лапласа в векторной формеИспользуя понятие векторного произведения, закон Био— Савара—Лапласа можно записать в векторной форме. В этом случае сразу будет определен и модуль вектора магнитной индукции Δ
Модуль магнитной индукции
как это и должно быть согласно закону (4.5.1). Направление Δ Магнитная индукция прямого тока
Для вычисления магнитной индукции бесконечно длинного прямого провода в произвольной точке А, находящейся на расстоянии d от провода, нужно просуммировать векторы Δ
Формула (4.5.5) дает правильное значение магнитной индукции и для прямого провода конечной длины. Необходимо только, чтобы расстояние d было много меньше длины провода и точка, в которой определяется индукция поля, находилась на большом расстоянии от концов провода.
|
|
|



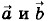 применяется косой крест:
применяется косой крест: 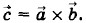 Если в результате скалярного произведения двух векторов получается скаляр, то результатом векторного произведения векторов является вектор (отсюда и его название). Определяется векторное произведение так.
Если в результате скалярного произведения двух векторов получается скаляр, то результатом векторного произведения векторов является вектор (отсюда и его название). Определяется векторное произведение так.
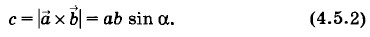
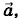 стоящего первым в векторном произведении, к вектору
стоящего первым в векторном произведении, к вектору 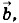 то вектор
то вектор 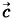 направлен в сторону поступательного перемещения буравчика. Таким образом, вектор с перпендикулярен плоскости, содержащей векторы
направлен в сторону поступательного перемещения буравчика. Таким образом, вектор с перпендикулярен плоскости, содержащей векторы 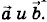

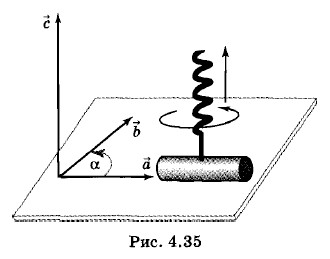
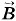 и его направление:
и его направление:

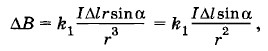
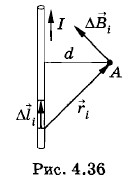
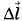 i (рис. 4.36). Суммирование упрощается благодаря тому, что векторы Δ
i (рис. 4.36). Суммирование упрощается благодаря тому, что векторы Δ