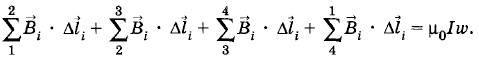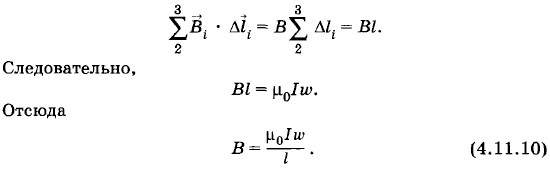|
|
|
|
|
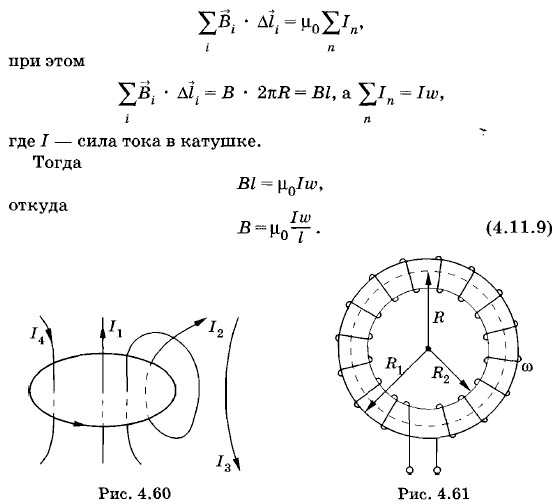
Глава 4. Магнитное поле токов § 4.11. Примеры решения задач (окончание)Задача 5Используя формулу Циркуляцией вектора магнитной индукции вдоль замкнутого контура называется сумма
где
Решение. Выберем замкнутый контур в виде окружности радиусом d, через центр которой проходит перпендикулярно плоскости окружности данный проводник. Тогда индукция во всех точках контура одинакова по модулю и направлена по касательной к окружности. Это ясно из соображений симметрии и вытекает из закона Био—Савара—Лапласа. Поэтому скалярные произведения Можно доказать, что в самом общем случае циркуляция вектора индукции магнитного поля по замкнутому контуру равна магнитной постоянной μ0, умноженной на алгебраическую сумму сил токов, охватываемых этим контуром:
Эта формула является математическим выражением теоремы о циркуляции вектора магнитной индукции.
Знак силы тока In определяется по ранее установленным правилам (см. гл. 2). Положительное направление тока связывают с направлением обхода контура правилом правого винта (буравчика).
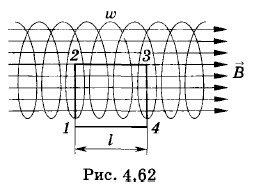
Каждый ток считается столько раз, сколько раз он охватывается контуром. Для системы токов, изображенных на рисунке 4.60,
Вычислите индукцию магнитного поля: а) внутри кольцевой катушки с током; б) внутри цилиндрической катушки.
Решение, а) На рисунке 4.61 изображена кольцевая катушка (тороид), имеющая б) На рисунке 4.62 изображена цилиндрическая катушка (соленоид), длина L которой во много раз больше диаметра D его витков. Такой соленоид можно практически считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него. Вне соленоида Для вычисления магнитной индукции внутри соленоида выделим на оси участок длиной l, на котором расположено ω витков, и проведем контур 1—2—3—4—1 (см. рис. 4.62).
Применяя теорему о циркуляции к этому контуру, получим:
На участках 1—2 и 3—4 элементы контура перпендикулярны линиям индукции, поэтому первое и третье слагаемые равны нулю. На участке 4—1 Формула (4.11.10) справедлива для достаточно длинного соленоида (D << L) вдали от его краев. При приближении к концам соленоида линии индукции начинают расходиться и значение модуля вектора
|
|
|



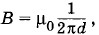 покажите, что циркуляция вектора магнитной индукции вдоль контура, охватывающего проводник с током, равна произведению магнитной постоянной μ0 на силу тока I в проводнике.
покажите, что циркуляция вектора магнитной индукции вдоль контура, охватывающего проводник с током, равна произведению магнитной постоянной μ0 на силу тока I в проводнике.
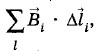
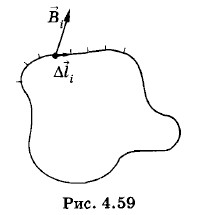
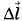 i — элемент контура, а
i — элемент контура, а 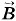 i — вектор магнитной индукции в соответствующей точке контура (рис. 4.59).
i — вектор магнитной индукции в соответствующей точке контура (рис. 4.59).
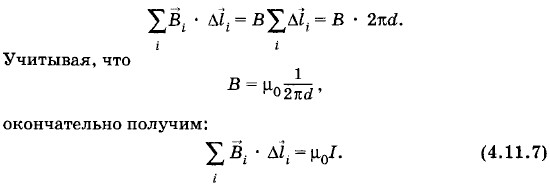
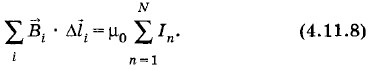
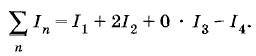
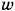 витков, которые распределены равномерно. Проведем контур в виде окружности радиусом R, совпадающей со средней линией магнитной индукции катушки (R2 < R < R1). Запишем для этого контура теорему о циркуляции вектора магнитной индукции:
витков, которые распределены равномерно. Проведем контур в виде окружности радиусом R, совпадающей со средней линией магнитной индукции катушки (R2 < R < R1). Запишем для этого контура теорему о циркуляции вектора магнитной индукции: