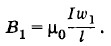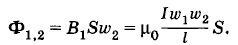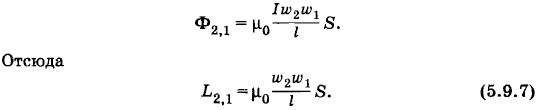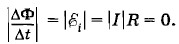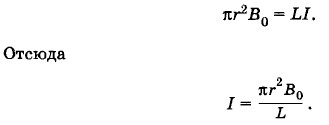§ 5.9. Примеры решения задач (окончание)

Задача 4

Из провода длиной l изготовили соленоид длиной l₀. Диаметр соленоида d << l₀. Определите индуктивность соленоида.

Решение. Согласно формуле (5.7.1) поток магнитной индукции Ф сквозь соленоид, в обмотке которого создан ток I, равен:

Ф = LI,

где L — искомая индуктивность.

Поток магнитной индукции

Ф = BS,

где В — индукция магнитного поля соленоида, S — площадь его поперечного сечения, — число витков соленоида. Если d << l₀, то магнитная индукция соленоида определяется по формуле (4.11.10):

Задача 5

Поверх длинного соленоида, имеющего ₁ витков, длину l и площадь сечения S, вплотную намотан по всей длине второй соленоид, имеющий ₂ витков и приблизительно такую же площадь сечения S. Определите взаимную индуктивность соленоидов.

Решение. Первый соленоид создает магнитное поле, индукция которого равна:

Это поле создает сквозь второй соленоид магнитный поток Ф_1,2, равный:

Отсюда для взаимной индуктивности L_1,2 получается выражение

Аналогично получаем выражение для потока магнитной индукции Ф_2,1 созданного вторым соленоидом и пронизывающего первый соленоид:

Из сравнения выражений (5.9.6) и (5.9.7) убеждаемся, что

L_1,2 = L_2,1.

Задача 6

Кольцо из сверхпроводника помещено в однородное магнитное поле, индукция которого нарастает от нуля до B₀. Плоскость кольца перпендикулярна линиям индукции магнитного поля. Чему равен индукционный ток, возникающий в кольце? Радиус кольца r, индуктивность L.

Решение. Так как сопротивление кольца R = 0, то, согласно закону Ома, и ЭДС в кольце всегда должна быть равна нулю. Это может быть только в том случае, если изменение полного магнитного потока, пронизывающего кольцо, равно нулю:

Так как Δt ≠ 0, то ΔФ = 0, т. е. Ф = const.

Следовательно, изменение внешнего магнитного потока Ф₀ равно по модулю и противоположно по знаку изменению магнитного потока, созданного индукционным током: ΔФ₀ = LΔI. Учитывая, что поток Ф₀ нарастает от 0 до πr2B₀, а индукционный ток меняется при этом от 0 до 7, получим:

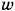<<< К началу параграфа