Уравнение теплового баланса без фазовых переходов

Будем считать тело однородным, то есть состоящим целиком из одного вещества (например, некоторая масса воды, стальной или медный брусок и т. д.). Рассмотрим сначала случай, когда агрегатное состояние тела не изменяется, то есть фазового перехода не происходит.

Из курса физики основной школы вы знаете, что в таком случае переданное телу количество теплоты Q прямо пропорционально массе тела т и изменению его температуры Δt:

Q = cmΔt. (2)

В этой формуле как Q, так и &Deltat могут быть как положительными, так и отрицательными величинами.

Входящую в эту формулу величину с называют удельной теплоёмкостью вещества, из которого состоит тело. Обычно в задачах на уравнение теплового баланса используют температуру по шкале Цельсия. Мы тоже будем так поступать.

1. На рисунке 48.1 приведены графики зависимости температуры двух тел от переданного им количества теплоты Q. Масса каждого тела 100 г.

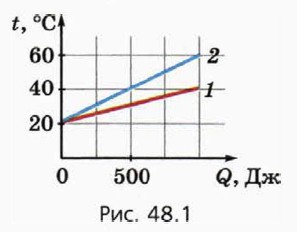
а) У какого тела удельная теплоёмкость больше и во сколько раз?

б) Чему равна удельная теплоёмкость каждого тела?

Рис. 48.1

2. В калориметр, содержащий 150 г воды при температуре 20 °С, погружают вынутый из кипятка металлический цилиндр. Удельная теплоёмкость воды равна 4,2 кДж/(кг • К). Примите, что тепловыми потерями можно пренебречь.

а) Объясните, почему справедливо уравнение

с_Мm_М(t_К - 100°) + c_Bm_B(t_K - 20°) = 0,

где с_М и с_В — значения теплоёмкости данного металла и воды соответственно, m_М и m_В — значения массы цилиндра и воды соответственно, t_K — значение конечной температуры содержимого калориметра, когда в нём установится тепловое равновесие.

б) Какое из двух слагаемых в приведённой формуле положительно, а какое — отрицательно? Поясните ваш ответ.

в) Чему равна удельная теплоёмкость данного металла, если масса цилиндра 100 г, а конечная температура равна 25 °С?

г) Чему равна конечная температура, если цилиндр изготовлен из алюминия, а его масса 100 г? Удельная теплоёмкость алюминия равна 0,92 кДж(Дкг • К).

д) Чему равна масса цилиндра, если он изготовлен из меди и его конечная температура 27 °С? Удельная теплоёмкость меди 0,4 кДж/(кг • К).

Окончание >>>