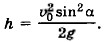|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Движение с постоянным ускорением свободного падения
Однако удобнее найти уравнение траектории, т. е. зависимость у от х. Чтобы получить это уравнение, нужно исключить время из уравнений (1.20) и (1.21). Из уравнения (1.20) имеем
Введём обозначения: tgα = с и
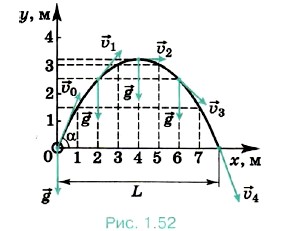
Из курса алгебры известно, что графиком функции (1.22) является парабола, ось симметрии которой — прямая, параллельная оси Y. Поскольку в данном случае b < 0, то ветви параболы направлены вниз. На рисунке 1.52 изображена парабола для случая b = -0,2 м-1 и с = 1,6.
Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе. Теперь определим дальность и максимальную высоту полёта тела.
Дальность полёта L = (υ0cosα)tпол. (1.23) Время полёта можно определить из уравнения (1.21). При падении тела у = 0, отсюда Время подъёма Из формул (1.20) и (1.21) видно, что движение тела, брошенного под углом к горизонту, можно рассматривать как сумму двух независимых движений — равномерного движения вдоль оси ОХ и равноускоренного движения вдоль оси OY.
Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально.
|
|
|



 Приведите ещё примеры ситуаций, в которых тело начинает падать с начальной скоростью, направленной под углом к горизонту.
Приведите ещё примеры ситуаций, в которых тело начинает падать с начальной скоростью, направленной под углом к горизонту.
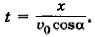 Следовательно,
Следовательно,
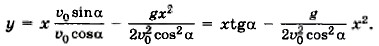
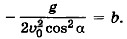 Следовательно,
Следовательно,

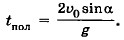 Подставив это выражение в уравнение (1.23), получим
Подставив это выражение в уравнение (1.23), получим 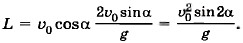
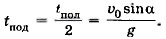 Подставив это выражение в уравнение (1.21), получим
Подставив это выражение в уравнение (1.21), получим