|
|
|
|
|
Глава 4. Закон сохранения импульса Импульс материальной точки. Закон сохранения импульсаЗакон сохранения импульсаПусть система состоит из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.
Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола — внешние силы. Пусть на тела некоторой системы действуют внешние силы F1 и F2 (рис. 4.2).
Обозначим внутренние силы через
Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за малый промежуток времени At, то для тел системы можно записать второй закон Ньютона в виде Δ Сложив эти равенства, получим Δ В левой части равенства (4.4) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса самой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы): Δ По третьему закону Ньютона
Учитывая равенства (4.4) и (4.6), можно записать: Δ где Мы доказали весьма важное положение:
Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут. Уравнение (4.7) справедливо для любого интервала времени Δt, если сумма внешних сил остаётся постоянной. Из уравнения (4.7) вытекает закон сохранения импульса.
Полученный результат справедлив для системы, содержащей произвольное число тел: m1 где Импульс, очевидно, сохраняется в изолированной системе тел, так как в этой системе на тела вообще не действуют внешние силы. Но область применения закона сохранения импульса шире. 1) Если даже на тела системы действуют внешние силы, но их сумма равна нулю, то импульс системы всё равно сохраняется. 2) Если сумма внешних сил не равна нулю, но сумма проекций сил на какое- то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется. 3) Если внешние силы много меньше внутренних сил, то можно считать, что импульс системы сохраняется. Например, при разрыве снарядов силы, разрывающие снаряд, много больше внешней силы тяжести.
|
|
|



 Обсудите с одноклассником, в каком случае импульс системы движущихся тел может быть равен нулю.
Обсудите с одноклассником, в каком случае импульс системы движущихся тел может быть равен нулю.
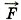 1, 2 и
1, 2 и 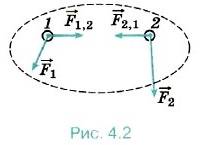
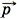 1 = (
1 = (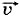 1 + m2
1 + m2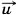 1 + m2
1 + m2