|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Равномерное прямолинейное движение. Скорость. Уравнение движенияУравнение равномерного прямолинейного движения точкиПусть радиус-вектор
Если начальный момент времени t0 принять равным нулю, то
Отсюда
Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий её положение в начальный момент времени. Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор
Выберем оси координат так, чтобы точка двигалась по какой-либо оси, например по оси ОХ. Тогда векторы х = х0 + υxt. (1.5)
Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х0. Если x = x0 + y = y0 z = z0, где х0, у0, z0 — проекции радиус-вектора
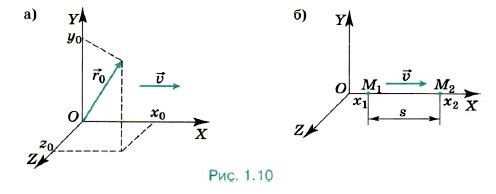
Путь s, пройденный точкой при движении вдоль оси ОХ (рис. 1.10, б), равен модулю изменения её координаты: s = |х2 - х1|. Его можно найти, зная модуль скорости υ = |υx|: s = |υx|t = υt. (1.6) Движение точки может происходить как по направлению оси ОХ (υx = υ), так и в противоположную сторону (υx = -υ). Поэтому при расчётах разумно пользоваться уравнением: х = х0 ± υt.
Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
|
|
|



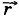 0 задаёт положение точки в начальный момент времени t0, а радиус-вектор
0 задаёт положение точки в начальный момент времени t0, а радиус-вектор 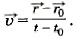
 Проведите эксперимент. Измерьте время вашего перемещения из одной точки в другую, например от двери школы до калитки. Определите скорость. Сравните вашу скорость со скоростью товарища, прошедшего это же расстояние.
Проведите эксперимент. Измерьте время вашего перемещения из одной точки в другую, например от двери школы до калитки. Определите скорость. Сравните вашу скорость со скоростью товарища, прошедшего это же расстояние.
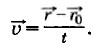
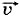 t. (1.4)
t. (1.4)
 Запишите уравнение (1.4) в проекциях на оси декартовой системы координат. Обсудите, в каком случае при рассмотрении движения точки можно ограничиться одной осью.
Запишите уравнение (1.4) в проекциях на оси декартовой системы координат. Обсудите, в каком случае при рассмотрении движения точки можно ограничиться одной осью.