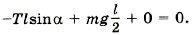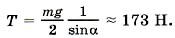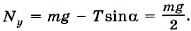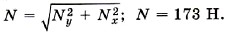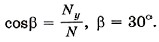|
|
|
|
|
Глава 7. Равновесие абсолютно твёрдых тел § 52. Примеры решения задач по теме «Равновесие твёрдых тел» (продолжение)Р е ш е н и е. На дверь люка действуют три силы (рис. 7.6, б): сила тяжести m
Выберем оси координат так, как показано на рисунке (7.6, б). Поскольку дверь находится в равновесии, то сумма моментов всех сил относительно, например, шарнира равна нулю: М1 + М + М2 = 0. Здесь M1, М, М2 — моменты сил Значит, М1 = -Tlsinα, Теперь запишем правило моментов сил, учитывая знаки этих моментов: Отсюда находим силу натяжения верёвки:
Для нахождения силы реакции шарнира воспользуемся первым условием равновесия: m Запишем это векторное уравнение в проекциях на координатные оси: —Тх + Nx = 0, Ту + Ny - mg = 0, или Nх = Тcosα, Отсюда Nх = 86,5 H; Nхy = 150 H. Модуль силы N равен Угол, который образует сила
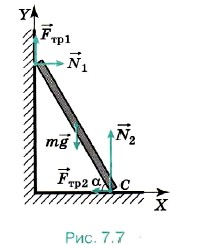
Задача 3. Лестница прислонена к стене. При каком минимальном угле наклона к полу она не будет падать? Коэффициенты трения между лестницей и стеной и между лестницей и полом соответственно равны μ1 и μ2. Р е ш е н и е. На лестницу действуют следующие силы (рис. 7.7): тяжести m
Первое условие равновесия для лестницы имеет вид m
|
|
|



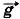 , приложенная к середине двери в точке D, сила натяжения
, приложенная к середине двери в точке D, сила натяжения 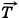 со стороны верёвки и сила реакции
со стороны верёвки и сила реакции 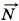 со стороны шарнира.
со стороны шарнира.
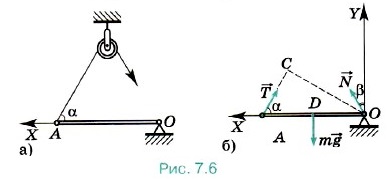
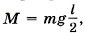 М2 = 0.
М2 = 0.