|
|
|
|
|
Глава 9. Молекулярно-кинетическая теория идеального газа Основное уравнение молекулярно-кинетической теории газовС самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и движутся они очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит движение всех молекул газа. Характер движения всей совокупности молекул газа известен из опыта. Молекулы участвуют в беспорядочном (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул беспрестанно меняется при их столкновениях друг с другом. Скорости отдельных молекул могут быть любыми, однако среднее значение модуля этих скоростей вполне определённое. В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости — средняя квадратичная скорость. От этой величины зависит средняя кинетическая энергия молекул. А средняя кинетическая энергия молекул, как мы вскоре убедимся, имеет очень большое значение во всей молекулярно-кинетической теории. Обозначим модули скоростей отдельных молекул газа через υ1, υ2, υ3, ... , υN. Среднее значение квадрата скорости определяется следующей формулой:
где N — число молекул в газе. Но квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат OX, OY, OZ. Из курса механики известно, что при движении на плоскости υ2 = υ2x + υ2y. В случае, когда тело движется в пространстве, квадрат скорости равен: υ2 = υ2x + υ2y + υ2z. (9.2)
Средние значения величин υ2x, υ2y и υ2z можно определить с помощью формул, подобных формуле (9.1). Между средним значением
Действительно, для каждой молекулы справедливо равенство (9.2). Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул N, мы придём к формуле (9.3).
Учитывая соотношение (9.4), подставим в формулу (9.3)
т. е. средний квадрат проекции скорости равен
Основное уравнение молекулярно-кинетической теории (МКТ) газовСтрогий вывод уравнения молекулярно-кинетической теории газов довольно сложен. Поэтому мы ограничимся упрощённым выводом уравнения. Предположим, что газ идеальный и взаимодействие молекул со стенкой абсолютно упругое. Вычислим давление газа, находящегося в сосуде, на боковую стенку площадью S, перпендикулярную координатной оси ОХ (рис. 9.2).
При ударе молекулы о стенку её импульс изменяется: Δрх = m0(υх - υ0x). При абсолютно упругом взаимодействии модули скорости молекулы до и после удара равны, и тогда изменение импульса Δрх = 2m0υx. Согласно второму закону Ньютона изменение импульса молекулы равно импульсу подействовавшей на неё силы со стороны стенки сосуда, а согласно третьему закону Ньютона импульс силы, с которой молекула подействовала на стенку, будет иметь то же значение.
|
|
|



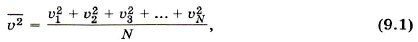
 Проведите числовой эксперимент. Пусть скорости молекул некоторого газа распределены так, как показано в таблице.
Проведите числовой эксперимент. Пусть скорости молекул некоторого газа распределены так, как показано в таблице.

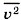 и средними значениями квадратов проекций существует такое же соотношение, как соотношение (9.2):
и средними значениями квадратов проекций существует такое же соотношение, как соотношение (9.2):


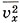 вместо
вместо 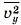 и
и 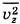 . Тогда для среднего квадрата проекции скорости на ось ОХ получим
. Тогда для среднего квадрата проекции скорости на ось ОХ получим

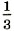 среднего квадрата самой скорости. Множитель
среднего квадрата самой скорости. Множитель 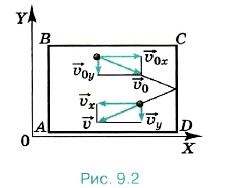
 Уравнение молекулярно-кинетической теории — первое количественное соотношение, полученное в МКТ, поэтому оно называется основным. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.
Уравнение молекулярно-кинетической теории — первое количественное соотношение, полученное в МКТ, поэтому оно называется основным. После вывода этого уравнения в XIX в. и экспериментального доказательства его справедливости началось быстрое развитие количественной теории, продолжающееся по сегодняшний день.