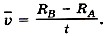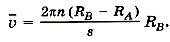|
|
|
|
|
Глава 9. Молекулярно-кинетическая теория идеального газа
Измерение скоростей молекул газа
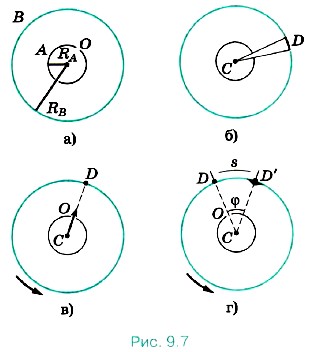
По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель О. Воздух из цилиндров откачан. Цилиндр В находится при комнатной температуре. Вначале прибор неподвижен. При прохождении тока по нити она нагревается и при температуре 1200 °С атомы серебра испаряются. Внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель О и, достигнув внутренней поверхности цилиндра В, осаждаются на ней. В результате прямо против щели образуется узкая полоска D серебра (рис. 9.7, б).
Затем цилиндры приводят во вращение с большим числом оборотов n в секунду (до 1500 1/c). Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров RB - RА, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадают на внутреннюю поверхность большого цилиндра не прямо против щели О (рис. 9.7, в), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 9.7, г): ведь атомы движутся прямолинейно. Если через υB обозначить модуль скорости вращения точек поверхности внешнего цилиндра, то s = υBt = 2 πnRBt. (9.20) В действительности атомы серебра имеют разные скорости. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полосках D и D' с наибольшей толщиной слоя серебра. Этому расстоянию будет соответствовать средняя скорость атомов, которая равна Подставляя в эту формулу значение времени t из выражения (9.20), получаем
Зная n, RA и RB и измеряя среднее смещение полоски серебра, вызванное вращением прибора, можно найти среднюю скорость атомов серебра. Модули скоростей, определённые из опыта, совпадают с теоретическим значением средней квадратичной скорости. Это служит экспериментальным доказательством справедливости формулы (9.19), а следовательно, и формулы (9.16), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.
|
Как вы думаете, почему проволочка сделана из платины?
|
|