|
|
|
|
|
Глава 14. Электростатика Потенциал электростатического поля и разность потенциаловСогласно данному определению потенциал равен:
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
Напряжённость поля Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
Разность потенциаловПодобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.
Так как потенциальная энергия Wn = дчр, то работа сил поля равна: А = - (Wп2 - Wп1) = -q(φ2 - φ1) = q(φ1 - φ2) = qU. (14.17) Здесь U = φ1 - φ2 — (14.18) разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:
Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
|
|
|



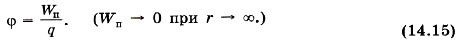
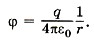
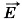 — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
— векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.

