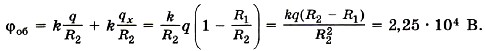|
|
|
|
|
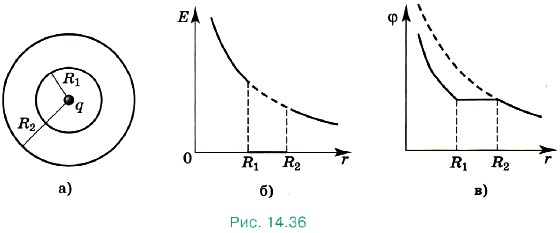
Глава 14. Электростатика Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов»Задача 4. В центр незаряженной металлической сферической оболочки с внутренним радиусом R1 и внешним радиусом R2 помещают заряд q (рис. 14.36, а). Определите напряжённость и потенциал поля как функции расстояния от центра сферы. Р е ш е н и е. Если заряд находится в центре, на внутренней поверхности металлической оболочки индуцируется заряд противоположного знака, а на внешней — того же знака, что и заряд q. При этом сумма индуцированных зарядов равна нулю (закон сохранения заряда). Силовые линии поля начинаются на заряде q и заканчиваются на внутренней поверхности оболочки, а затем опять начинаются на внешней поверхности оболочки. Напряжённость электрического поля внутри проводника равна нулю. Картина силовых линий поля данной системы аналогична картине силовых линий поля точечного заряда за исключением области, занимаемой оболочкой. Здесь силовые линии терпят разрыв.
На рисунке 14.36, б изображена зависимость напряжённости Е(r).
Согласно принципу суперпозиции потенциал любой точки поля складывается из потенциала поля заряда q, проводящей сферы радиусом R1, с зарядом -q и проводящей сферы радиусом R2 с зарядом +q.
На рисунке 14.36, в изображена зависимость потенциала φ(r). Задача 5. Металлический шарик радиусом R1 = 20 см окружили тонкой сферической заряженной оболочкой, радиус которой R2 = 40 см и заряд q = 2 • 10-6 Кл (рис. 14.37). Определите потенциал оболочки и заряд шарика после того, как его заземлили.
Р е ш е н и е. После заземления шарика в системе будет происходить перетекание заряда до тех пор, пока потенциал шарика не станет равным нулю. Потенциал шарика Запишем выражение для потенциала оболочки и подставим в него выражение для заряда qx шарика:
|
|
|



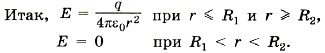
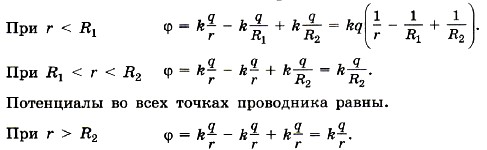
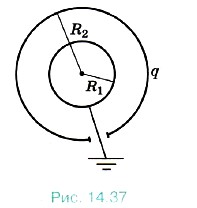
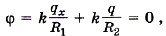 где qx — заряд шарика. Отсюда qx = -qR1/R2 = -10-6 Кл.
где qx — заряд шарика. Отсюда qx = -qR1/R2 = -10-6 Кл.