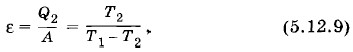|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 5. Законы термодинамики § 5.12. Максимальный КПД тепловых двигателей
Идеальная тепловая машина КарноКарно придумал идеальную тепловую машину с идеальным газом в качестве рабочего тела. Все процессы в машине Карно рассматриваются как равновесные (обратимые).
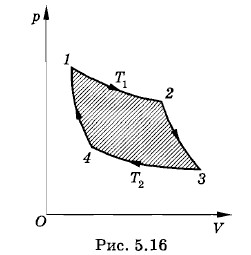
В машине осуществляется круговой процесс или цикл, при котором система после ряда преобразований возвращается в исходное состояние. Цикл Карно состоит из двух изотерм и двух, адиабат (рис. 5.16). Кривые 1 —2 и 3—4 — это изотермы, а 2—3 и 4—1 — адиабаты. Сначала газ расширяется изотермически при температуре T1. При этом он получает от нагревателя количество теплоты Q1. Затем он расширяется адиабатно и не обменивается теплотой с окружающими телами. Далее следует изотермическое сжатие газа при температуре Т2. Газ отдает в этом процессе холодильнику количество теплоты Q2. Наконец газ сжимается адиабатно и возвращается в начальное состояние. При изотермическом расширении газ совершает работу А'1 > 0, равную количеству теплоты Q1. При адиабатном расширении 2—3 положительная работа А'3 равна уменьшению внутренней энергии при охлаждении газа от температуры T1 до температуры Т2: А'3 = -ΔU12 = U(Т1) - U (Т2). Изотермическое сжатие при температуре Т2 требует совершения над газом работы А2. Газ совершает соответственно отрицательную работу А2 = -А2 = Q2. Наконец, адиабатное сжатие требует совершения над газом работы А4 = ΔU21. Работа самого газа А'4 = -A4 = -ΔU21 = U(T2) - U(T1). Поэтому суммарная работа газа при двух адиабатных процессах равна нулю. За цикл газ совершает работу А' = А'1 + А'2 = Q1 + Q2 = |Q1| — |Q2|. (5.12.1) Эта работа численно равна площади фигуры, ограниченной кривой цикла (заштрихована на рис. 5.16). Для вычисления коэффициента полезного действия нужно вычислить работы при изотермических процессах 1 —2 и 3—4. Расчеты приводят к следующему результату:
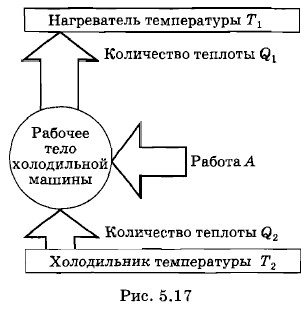
Коэффициент полезного действия тепловой машины Карно равен отношению разности абсолютных температур нагревателя и холодильника к абсолютной температуре нагревателя. Можно выразить работу, совершаемую машиной за цикл, и количество отданной холодильнику теплоты Q2 через КПД машины и полученное от нагревателя количество теплоты Q1. Согласно определению КПД A' = ηQ1. (5.12.3) Количество теплоты Q2 = А' - Q, = ηQ1 - Q1 = Q1(η - 1). (5.12.4) Так как η < 1, то |Q2| = (1 - η)Q1. (5.12.5) Идеальная холодильная машинаЦикл Карно обратим, поэтому его можно провести в обратном направлении. Это будет уже не тепловая машина, а идеальная холодильная машина. Процессы пойдут в обратном порядке. Работа А совершается для приведения в действие машины. Количество теплоты Q1 передается рабочим телом нагревателю более высокой температуры, а количество теплоты Q2 поступает к рабочему телу от холодильника (рис. 5.17). Теплота передается от холодного тела к горячему, поэтому машина и называется холодильной. Но второму закону термодинамики это не противоречит: теплота переходит не сама собой, а за счет совершения работы.
Выразим количества теплоты Q1 и Q2 через работу А и КПД машины η. Так как согласно формуле (5.12.3) А' = ηQ1 = -А, то
Передаваемое рабочим телом количество теплоты, как всегда отрицательно. Очевидно,
Такое количество теплоты получает рабочее тело от холодильника. Холодильная машина работает как тепловой насос*. Горячему телу передается количество теплоты Q1, большее того количества, которое забирается от холодильника. Согласно формуле (5.12.7) |Q1| = A + Q2. (5.12.8) * Однако это не означает, что холодильная машина и тепловой насос — это одно и то же. Назначение холодильной машины — охлаждать некоторый резервуар, передавая теплоту в окружающую среду. Назначение теплового насоса — нагревать резервуар, забирая теплоту из окружающей среды. Эффективность холодильной машины определяется отношением
т. е. холодильный коэффициент тем больше, чем меньше разность температур, и тем меньше, чем меньше температура того тела, от которого отбирается теплота. Очевидно, холодильный коэффициент может быть больше единицы. Для реальных холодильников он более трех. Разновидностью холодильной машины является кондиционер, который забирает теплоту из комнаты и передает ее окружающему воздуху.
|
|
|





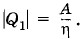 Согласно выражению (5.12.4) количество теплоты Q2 = Q1(η - 1) или с учетом соотношения (5.12.3)
Согласно выражению (5.12.4) количество теплоты Q2 = Q1(η - 1) или с учетом соотношения (5.12.3)

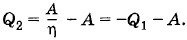 Отсюда
Отсюда
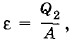 так как ее назначение отнимать как можно большее количество теплоты от охлаждаемой системы при совершении как можно меньшей работы. Величина ε называется холодильным коэффициентом. Для идеальной холодильной машины согласно формулам (5.12.7) и (5.12.2)
так как ее назначение отнимать как можно большее количество теплоты от охлаждаемой системы при совершении как можно меньшей работы. Величина ε называется холодильным коэффициентом. Для идеальной холодильной машины согласно формулам (5.12.7) и (5.12.2)