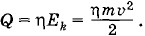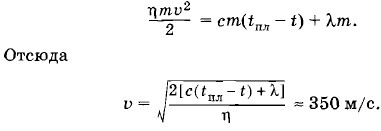|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 8. Твердые тела и их превращение в жидкости Примеры решения задач на тему: Твердые тела и их превращение в жидкостиПри решении большинства задач на материал § 8.9 используется уравнение теплового баланса Решение ряда задач требует знания кристаллической структуры вещества. Задача 1
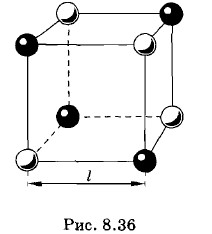
Кристаллы поваренной соли состоят из чередующихся ионов натрия и хлора, причем ячейка кристалла имеет форму куба (рис. 8.36). Определите средние расстояния между центрами ионов в ячейке. Молярная масса поваренной соли 0,058 кг/моль, а ее плотность 2200 кг/м3. Решение. Кубическая ячейка поваренной соли NaCl состоит из четырех ионов Na и четырех ионов Сl, находящихся в ее вершинах. Каждый ион (Na или Сl) входит в состав восьми ячеек. Поэтому в кристалле NaCl число кубических ячеек равно суммарному числу ионов Na и Сl. Следовательно, в одном моле поваренной соли содержится 2NA ячеек, где NA— постоянная Авогадро. Обозначим искомое расстояние между ионами Na и Сl в ячейке буквой l, тогда объем ячейки будет равен l3. Объем одного моля (молярный объем) поваренной соли равен VM = l3 • 2NA. (8.10.1) С другой стороны, молярный объем поваренной соли можно найти, разделив молярную массу на плотность:
Из выражений (8.10.1) и (8.10.2) получаем
Задача 2В массивный алюминиевый сосуд, нагретый до температуры t1 = 75 °С, положили лед массой m2 = 0,4 кг при температуре t2 = 0 °С. После установления теплового равновесия температура сосуда с его содержимым оказалась равной t = = 50 °С. Какова масса m1 сосуда? Удельные теплоемкоёти алюминия и воды соответственно равны с1 = 770 Дж/(кг • К) и с2 = 4200 Дж/(кг • К). Удельная теплота плавления льда λ = 3,35 • 105 Дж/кг. Испарением воды и потерями тепла пренебречь. Решение. Количество теплоты, отданное остывающим сосудом, Q1 = c1m1(t - t1) отрицательно, так как t < t1. На плавление льда пошло количество теплоты Q2 = λm2, а на нагревание образовавшейся воды от 0 °С до температуры t — количество теплоты Q3 = с2m2(t - t2), Уравнение теплового баланса записывается в виде Q1 + Q2 + Q3 = О, или c1m1(t - t1) + λт2 + c2m2(t - t2) = 0. Откуда находим
Задача 3В калориметре находится вода массой m1 = 400 г при температуре t1 = 5 °С. К ней долили еще 200 г (m2) воды при температуре t2 = 10 °С и положили лед массой m3 = 400 г при температуре t3 = -60 °С. Какая температура t установится в калориметре? Удельные теплоемкости льда и воды соответственно равны сл = 2,1 • 103 Дж/(кг • К) и св = 4,2 • 103 Дж/(кг • К). Удельная теплота плавления льда λ = 3,35 • 105 Дж/кг. Решение. В этой и подобных ей задачах не следует торопиться составлять уравнение теплового баланса. Надо сначала выяснить, расплавится ли весь лед. Количество теплоты, которое выделяется водой при охлаждении до t0 = 0 °С, равно Q1 = cвm1(t1 - t0) + свm2(t2 - t0) = 16 800 Дж. Для нагревания льда до 0 °С требуется Q2 = c2m2(t0 - t3) = 50 400 Дж. Следовательно, лед может нагреваться до температуры плавления только за счет энергии, выделяющейся при замерзании воды. Для выделения недостающего количества теплоты Q3 = 33 600 Дж должна замерзнуть вода массой
В результате в калориметре образуется смесь из 500 г воды и 500 г льда, находящихся при температуре 0 °С. Задача 4С какой скоростью должна лететь свинцовая пуля, чтобы, ударившись о преграду, расплавиться, если до удара температура пули была t = 127 °С? При ударе на нагревание пули затрачивается η = 80% энергии пули (остальная энергия рассеивается в окружающее пространство). Удельная теплоемкость свинца с = 120 Дж/(кг • К), температура плавления свинца tпл = 327 °С. Удельная теплота плавления λ = 2,5 • 104 Дж/кг. Решение. Кинетическая энергия летящей пули С другой стороны, на нагревание и плавление пули должно быть затрачено количество теплоты, равное Q = cm(tпл - t) + λm. Следовательно, согласно закону сохранения энергии
|
|
|



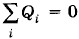 с включаемой в него теплотой плавления Qпл = λm или теплотой кристаллизации Qkp = -λm.
с включаемой в него теплотой плавления Qпл = λm или теплотой кристаллизации Qkp = -λm.

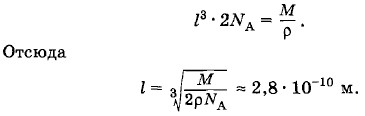
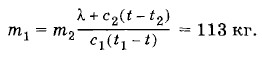
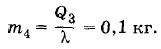
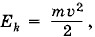 где m — масса пули, υ — ее скорость. На нагревание и плавление пули затрачивается энергия
где m — масса пули, υ — ее скорость. На нагревание и плавление пули затрачивается энергия