|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 9. Тепловое расширение твердых и жидких тел § 9.3. Тепловое объемное расширение
Измерения показывают, что в пределах не очень большого интервала температур можно считать, что относительное изменение объема пропорционально изменению температуры:
Коэффициент пропорциональности α называют температурным коэффициентом объемного расширения. Он показывает, на какую долю своего первоначального значения изменяется объем тела при изменении температуры на 1 К. Коэффициент объемного расширения, как и коэффициент линейного расширения, зависит от природы вещества и температуры. Зависимость α от температуры незначительна и ею можно пренебречь, если интервал изменения температуры невелик. Для большинства твердых тел коэффициент α имеет порядок 10-5—10-4К-1, т. е. очень мал по сравнению с коэффициентом объемного расширения газов. Из формулы (9.3.1) легко найти выражение для объема тела при любой температуре: V = V0(1 + αΔt). (9.3.2) В этой формуле значение начального объема V0 обычно берут при начальной температуре t0 = 0 °С. Однако и здесь, как в случае линейного расширения, можно пользоваться формулой V2 = V1(1 + αΔt), (9.3.3) где V1 — объем тела при температуре t1; V2 — объем тела при температуре t2; Δt = t2 - t1. Объем полого (пустого) твердого тела (сосуда) при нагревании увеличивается так, как если бы это тело было сплошным. Объем полости в твердом теле (сосуде) при его нагревании увеличивается так, как увеличивался бы объем тела, изготовленного из того же вещества и имеющего форму и размер полости. Связь между коэффициентами линейного и объемного расширенияКоэффициент линейного расширения α1 и коэффициент объемного расширения α связаны между собой. Эту связь можно найти, рассматривая тепловое расширение тела простой формы, например кубика с ребром l0. При нагревании кубика на Δt каждая его сторона увеличится на Δl и станет равной l = l0(1 + α1Δt). (9.3.4) Объем тела при этом будет равен V = V0(l + αΔt). Но
Подставляя Z из уравнения (9.3.4) в уравнение (9.3.5), получим
Так как величина α1 очень мала, то при малых изменениях температуры членами α ≈ Зα1. (9.3.6) Итак, температурный коэффициент объемного расширения равен утроенному коэффициенту линейного расширения.
|
|
|



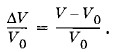
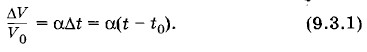
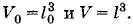 Следовательно,
Следовательно,

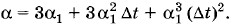
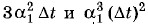 можно пренебречь по сравнению с членом 3α1. Поэтому
можно пренебречь по сравнению с членом 3α1. Поэтому