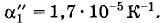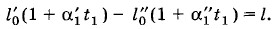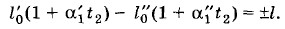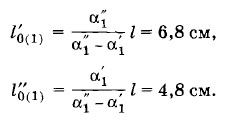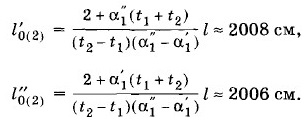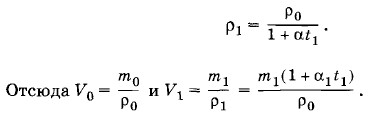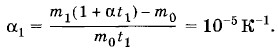|
|
|
|
Главная >> Молекулярная физика. Термодинамика. Физика 10 класс. Мякишев |
|
|
Глава 9. Тепловое расширение твердых и жидких тел § 9.5. Примеры решения задач на тему: Тепловое расширение твердых и жидких телЗадача 1Диаметр стеклянной пробки, застрявшей в горлышке флакона, d0 = 2,5 см. Чтобы вынуть пробку, горлышко нагрели до температуры t1 = 150 °С. Сама пробка успела при этом нагреться до температуры t2 = 50 °С. Как велик образовавшийся зазор? Температурный коэффициент линейного расширения стекла α1 = 9 • 10-6К-1. Решение. Обозначим начальную температуру стеклянного флакона и застрявшей в нем пробки через t0. Тогда после нагревания диаметр горлышка флакона будет d1 = d0[1 + α1(t1 — t0)], а диаметр пробки d2 = d0[1 + α1(t2 — t0)], Образовавшийся зазор между пробкой и горлышком составит
Подставляя числовые значения величин, найдем l = 0,01 мм. Задача 2Объем некоторой массы спирта при нагревании увеличился на ΔV = 5,5 см3. Начальная плотность спирта ρ0 = 800 кг/м3, температурный коэффициент объемного расширения спирта α = 1,1 • 10-3К-1. Удельная теплоемкость спирта с = 2,4 х 103 Дж/(кг • К). Какое количество теплоты сообщено спирту? Решение. Первоначальный объем спирта V0. После нагревания он стал равен V = V0(1 + αΔt). Изменение объема спирта ΔV = V - V0 = V0αΔt. (9.5.1) Количество теплоты, сообщенное спирту при нагревании, Q = cmΔt, (9.5.2) где m = p0V0 — масса спирта. Разделив почленно выражения (9.5.1) и (9.5.2), получим
Задача 3Как велика сила F, которую нужно приложить к медной проволоке с площадью поперечного сечения S = 10 мм2, чтобы растянуть ее на столько же, на сколько она удлиняется при нагревании на Δt = 20 К? Коэффициент линейного расширения меди α1 = 1,7 • 10-5К-1, модуль Юнга Е = 1,2 • 1011 Па. Решение. Согласно закону Гука σ = Еε или
Согласно условию задачи проволока должна получить такое же удлинение при нагревании на Δt: Δl = l0α1Δt (9.5.4) Подставив в уравнение (9.5.3) выражение (9.5.4) для Δl, получим выражение для силы: F = ESα1Δt = 410 Н. Задача 4Определите длины Решение. Разность длин линеек при температуре t1 равна
При температуре t2 эта разность равна
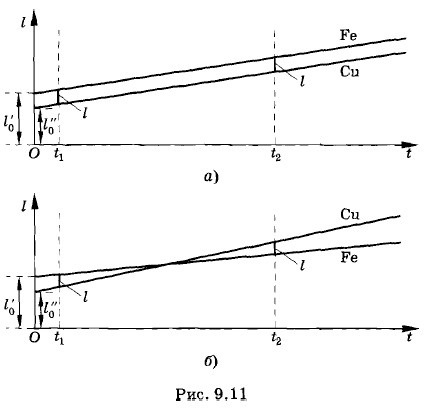
Знак плюс соответствует случаю, когда разность длин линеек остается неизменной (рис. 9.11, а). Знаку минус соответствует случай, когда при температурах t1 и t2 разности длин линеек одинаковы по модулю, но противоположны по знаку (рис. 9.11, б).
В первом случае система уравнений приводит к следующим результатам:
Во втором случае результаты получаются такими:
В обоих случаях при t0 = 0 °С длина железной линейки должна быть больше медной. Задача 5При температуре t0 = 0 °С стеклянный баллон вмещает m0 = 100 г ртути. При температуре t1 = 20 °С баллон вмещает m1 = 99,7 г ртути. В обоих случаях температура ртути равна температуре баллона. Найдите по этим данным температурный коэффициент линейного расширения стекла α1, учитывая, что коэффициент объемного расширения ртути α = 1,8 • 10-4К-1. Решение. Если вместимость баллона при 0 °С обозначить через V0, то при температуре t1 она будет равна V1 = V0(l + 3α1t1). (9.5.5)
Обозначим через ρ0 и ρ1 плотности ртути при температурах t0 и t1. Тогда массы ртути при начальной и конечной температурах будут равны m0 = ρ0V0 и m1 = ρ1V1, причем согласно формуле (9.3.7)
Из выражения (9.5.5) находим
Подставляя в уравнение (9.5.6) значения V0 и V1, окончательно получим
|
|
|



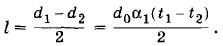
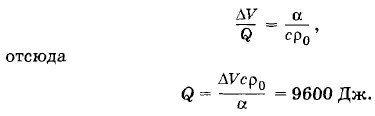
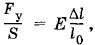 где Fy — сила упругости, возникающая в проволоке при ее относительном удлинении
где Fy — сила упругости, возникающая в проволоке при ее относительном удлинении 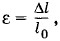 а. Е — модуль упругости (модуль Юнга) меди. Приложенная к проволоке сила равна по модулю силе упругости, поэтому
а. Е — модуль упругости (модуль Юнга) меди. Приложенная к проволоке сила равна по модулю силе упругости, поэтому
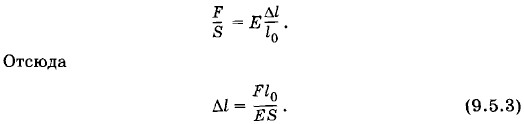
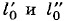 железной и медной линеек при температуре t0 = 0 °С, если разности их длин при температурах t1 = 50 °С и t2 = 450 °С одинаковы по модулю и равны l = 2 см. Коэффициенты линейного расширения железа и меди соответственно равны а
железной и медной линеек при температуре t0 = 0 °С, если разности их длин при температурах t1 = 50 °С и t2 = 450 °С одинаковы по модулю и равны l = 2 см. Коэффициенты линейного расширения железа и меди соответственно равны а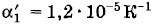 и
и