§ 2.5. Потенциальная энергия взаимодействия молекул

При изучении поведения большой совокупности молекул вместо силы взаимодействия молекул удобнее пользоваться потенциальной энергией.
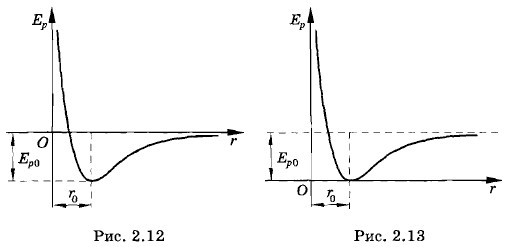
Нужно вычислять средние характеристики системы, а понятие средней силы взаимодействия молекул лишено смысла, так как сумма всех сил, действующих между молекулами, в соответствии с третьим законом Ньютона равна нулю. Средняя же потенциальная энергия в существенной мере определяет состояние и свойства вещества.

Зависимость потенциальной энергии от расстояния между молекулами

Так как изменение потенциальной энергии определяется работой силы, то по известной зависимости силы от расстояния можно найти зависимость от расстояния потенциальной энергии. Но нам достаточно знать лишь примерный вид потенциальной кривой Е_р (r). Прежде всего вспомним, что потенциальная энергия определяется с точностью до произвольной постоянной, потому что непосредственный смысл имеет не сама потенциальная энергия, а разность потенциальных энергий в двух точках, равная работе, взятой с противоположным знаком. Будем считать, как принято в физике, Е_р = 0 при r → ∞. Потенциальную энергию системы можно рассматривать как работу, которую система может совершить, причем потенциальная энергия определяется расположением тел, но не их скоростями. Чем больше расстояние между молекулами, тем большую работу совершат силы притяжения между ними при их сближении. Поэтому при уменьшении r, начиная от очень больших значений, потенциальная энергия будет уменьшаться. Мы приняли, что при r → ∞ потенциальная энергия равна нулю, следовательно, при уменьшении r потенциальная энергия становится отрицательной (рис. 2.12).

В точке r = r₀ сила равна нулю (см. рис. 2.10). Поэтому если молекулы расположены на этом расстоянии, то они будут покоиться, и никакую работу система совершать не может. Это означает, что при r = r₀ потенциальная энергия имеет минимум. Мы могли бы это значение потенциальной энергии Е_р0 принять за начало отсчета потенциальной энергии. Тогда она была бы всюду положительной (рис. 2.13). Обе кривые (см. рис. 2.12 и 2.13) одинаково характеризуют взаимодействие молекул. Разность значений Е_р для двух точек одинакова у обеих кривых, а только она и имеет смысл.

потенциальная энергия

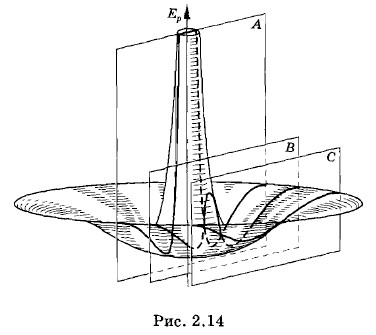
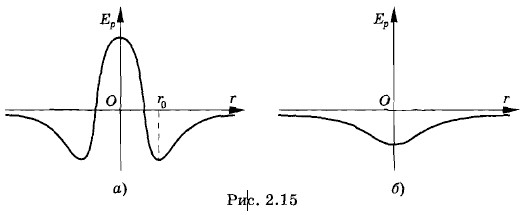
При r < r₀ появляются быстро растущие силы отталкивания. Они также могут совершать работу. Поэтому потенциальная энергия при дальнейшем сближении молекул растет, причем очень быстро.

Потенциальная кривая будет иметь форму, изображенную на рисунке 2.12, если молекулы сближаются в плоскости А вдоль линии, соединяющей их центры (рис. 2.14). Если же молекулы сближаются в плоскости В или в плоскости С, то потенциальная кривая будет иметь вид, показанный соответственно на рисунках 2.15,а и 2.15, б.

молекулы сближаются

потенциальная кривая

Главная задача

Можно многое объяснить и понять, исходя из определенных представлений о характере взаимодействия молекул в веществе. Мы остановимся только на одном очень общем вопросе: каким образом знание зависимости потенциальной энергии от расстояния между молекулами позволяет установить количественный критерий различия между газами, жидкостями и твердыми телами с точки зрения молекулярно-кинетической теории.

Предварительно рассмотрим движение молекул с энергетической точки зрения.

Движение частицы в пространстве с заданной потенциальной энергией

Зная зависимость потенциальной энергии от расстояния, можно установить характер движения тела, используя лишь закон сохранения энергии.

Пусть одна из молекул неподвижна, и мы рассматриваем движение другой молекулы. Характер движения молекулы зависит от ее полной энергии Е. Согласно закону сохранения энергии полная энергия молекулы остается постоянной:

Е = Е_к + Е_р, (2.5.1)

где Е_к и Е_р — соответственно кинетическая и потенциальная энергии молекулы.

Рассмотрим вначале случай, когда Е = Е₁ > 0 (рис. 2.16). Полную энергию можно характеризовать прямой, параллельной оси r, так как при любых r она имеет одно и то же значение. При движении молекулы вдоль оси r ее кинетическая и потенциальная энергии непрерывно изменяются: чем больше потенциальная энергия, тем меньше кинетическая и наоборот. Если частица движется справа налево, то ее кинетическая энергия растет и в точке r = r₀ (минимум потенциальной энергии) достигает максимума. С дальнейшим уменьшением r кинетическая энергия начинает убывать. В точке r = r₁ кинетическая энергия равна нулю, так как в этой точке полная энергия равна потенциальной. Попасть в область, где r < r₁, частица не может, так как при этом ее положительная потенциальная энергия оказалась бы больше полной энергии и, следовательно, кинетическая энергия сделалась бы отрицательной. Но кинетическая энергия всегда положительна.

В точке r = r₁ частица останавливается и начинает двигаться назад, ибо на нее действует сила отталкивания. Эта точка называется точкой поворота. В дальнейшем молекула движется в положительном направлении оси r и уходит в бесконечность.

Совершенно иная картина будет наблюдаться при Е = Е₂ < 0 (см. рис. 2.16). В этом случае молекула находится в потенциальной яме и не может из нее выйти. В точках поворота r₂ и r₃ кинетическая энергия равна нулю. Возникает так называемое связанное состояние: молекулы совершают колебания около друг друга.

Разделение системы на две независимые частицы невозможно без увеличения полной энергии до Е > 0.

Располагая графиком зависимости силы взаимодействия между молекулами от расстояния, можно установить, как зависит от расстояния потенциальная энергия. Зная зависимость потенциальной энергии от расстояния, можно выяснить характер движения молекул относительно друг друга.