|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 4. Равномерное прямолинейное движение. Скорость. Уравнение движения (окончание)Выберем оси координат так, чтобы точка двигалась по какой-либо оси, например по оси ОХ. Тогда векторы х = х0 + υxt. (1.5)
Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х0. Если x = x0 + где х0, у0, z0 — проекции радиус-вектора Путь s, пройденный точкой при движении вдоль оси ОХ (рис. 1.10, б), равен модулю изменения её координаты: s = |х2 - х1|. Его можно найти, зная модуль скорости υ = |υx|: s = |υx|t = υt. (1.6) Движение точки может происходить как по направлению оси ОХ (υx = υ), так и в противоположную сторону (υx = -υ). Поэтому при расчётах разумно пользоваться уравнением: х = х0 ± υt.
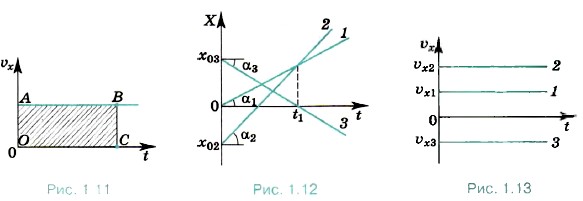
Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения. Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υx, а сторона ОС — время движения t, поэтому Δx = υxt.
На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х0 = 0, υx1 > 0; прямая 2 — случаю х0 < 0, υx2 > 0, а прямая 3 — случаю х0 > 0, υx3 < 0. Угол наклона α2 прямой 2 больше, чем угол наклона α1 прямой 1. За один и тот же промежуток времени t1 точка, движущаяся со скоростью υx2, проходит большее расстояние, чем при движении её со скоростью υx1. Следовательно, скорость υx2 больше, чем скорость υx1. Проекция скорости определяет угол наклона прямой к оси t. Очевидно, проекция скорости υx численно равна тангенсу угла α. В случае 3 α3 < 0, движение происходит в сторону, противоположную оси ОХ. На рисунке 1.13 представлены зависимости проекций скоростей от времени для случаев 1, 2 и 3.
Вопросы к параграфу 1. Как записывается в векторной форме уравнение равномерного прямолинейного движения точки? 2. Как записывается в координатной форме уравнение равномерного прямолинейного движения точки, если она движется: по оси OY? по оси OZ? 3. Равен ли модуль перемещения длине пути при равномерном движении точки? 4. Можно ли сказать, что тангенс угла наклона прямой x(t) к оси t численно равен скорости?
<<< К началу параграфа Следующая страница >>>
|
|
|



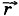 0 и
0 и 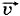 будут составлять с осями OY и OZ прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора
будут составлять с осями OY и OZ прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора 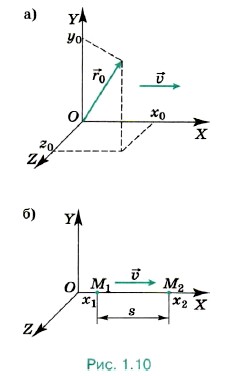
 Какое из наблюдаемых вами движений можно приблизительно считать равномерным?
Какое из наблюдаемых вами движений можно приблизительно считать равномерным?