§ 4.16. Интерференция волн

До сих пор мы почти все время имели дело с одной волной, распространяющейся от источника. Однако очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то отдельные звуковые волны накладываются друг на друга. Что при этом происходит?

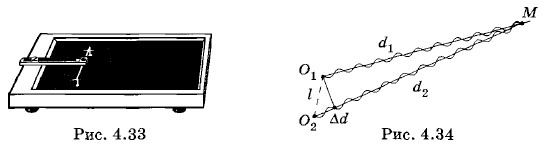
Проще всего проследить за этим явлением, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что Каждая волна проходит сквозь другую и ведет себя в дальнейшем так, будто другой волны совсем не существует. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны, возникающие на поверхности воды от двух камней, мы можем заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось.

Если две волны встречаются в одном месте гребнями, то в этом месте возмущение воды усиливается.

Если же, напротив, гребень одной волны встречается с впадиной другой, то возмущения поверхности воды не будет.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция

Сложение в пространстве двух (или нескольких) волн, при котором образуется постоянное во времени распределение амплитуды результирующих колебаний в различных точках пространства, называется интерференцией. Стоячая волна — пример интерференции двух волн, бегущих в противоположные стороны.

Выясним, при каких условиях происходит интерференция волн. Для этого рассмотрим более подробно наложение волн на поверхности воды.

Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, который совершает гармонические колебания (рис. 4.33). В любой точке М на поверхности воды (рис. 4.34) будут складываться колебания, вызванные двумя волнами (от источников O₁ и O₂). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, отличаться, так как волны проходят различные пути d₁ и d₂. Но если расстояние I между источниками много меньше этих путей (l << d₁ и l << d₂), то обе амплитуды можно считать практически одинаковыми.

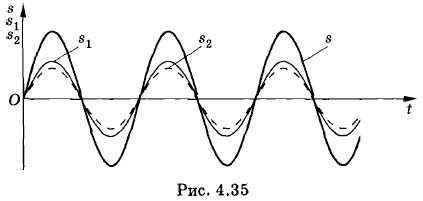
Результат сложения волн, приходящих в точку М, будет зависеть от разности фаз между ними. Пройдя различные расстояния d₁ и d₂, волны имеют разность хода Δd = d₂ - d₁ Если разность хода равна длине волны λ, то вторая волна будет запаздывать по сравнению с первой на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн будут совпадать.

Условие максимумов

На рисунке 4.35 изображена зависимость от времени смещений sx и s2, вызванных двумя волнами, при Δd = λ. Разность фаз колебаний равна нулю (или, что то же самое, 2π, так как период синуса равен 2π). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний среды в данной точке будет максимальной, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн*:

Δd = kλ, (4.16.1)

где k = 0, 1, 2, ... .

* Это справедливо лишь при условии, что фазы колебаний обоих источников совпадают.

Окончание параграфа >>>