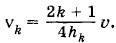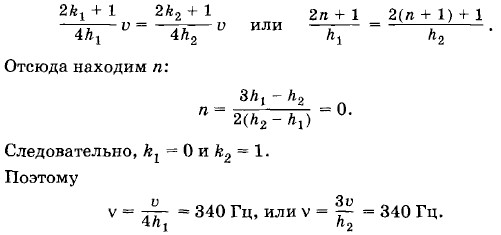|
|
|
|
|
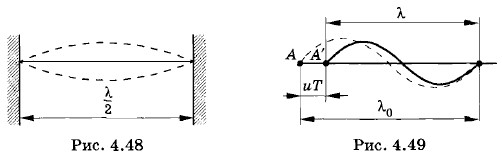
Глава 4. Механические волны. Звук § 4.20. Примеры решения задач на тему: Механические волныЗадача 4Найдите зависимость частоты колебаний основного тона струны от ее длины l, плотности ρ, площади поперечного сечения S и силы натяжения F. Решение. При возбуждении колебаний струны на ней устанавливается стоячая волна (рис. 4.48). Длина волны X основного тона равна:
Задача 5Движущийся по реке теплоход дает свисток, частота которого νO = 400 Гц. Стоящий на берегу наблюдатель воспринимает звук свистка как колебания с частотой ν = 395 Гц. С какой скоростью u движется теплоход? Приближается или удаляется он от наблюдателя? Скорость звука υ принять равной 340 м/с. Решение. Частота звука зависит от скорости движения источника. При неподвижном источнике (точка А на рисунке 4.49) за время, равное периоду колебаний Т, колебание распространится на расстояние, равное длине волны λ0 = υT. Если же источник движется (точка А' на рисунке 4.49) со скоростью и, то за время Т он пройдет в направлении распространения волны путь uТ, и колебание распространится за это время на расстояние λ = λ0 - uТ = (υ - u)Т. При удаляющемся источнике λ = (υ + u)Т. Таким образом, частота колебаний, воспринимаемых ухом неподвижного человека, от движущегося источника звука получается равной
Это выражение можно упростить, если u << υ. Для этого умножим числитель и знаменатель на (υ ± u) и пренебрежем членом
Знаку «+» соответствует приближение источника, а знаку «-» — удаление. Это явление носит название эффекта Доплера. Согласно условию задачи ν < ν0, следовательно, теплоход удаляется от берега. Искомая скорость
Задача 6К верхнему концу цилиндрического сосуда, в который постепенно наливают воду, поднесен звучащий камертон. .Звук, издаваемый камертоном, заметно усиливается, когда расстояния от поверхности жидкости до верхнего края сосуда достигают значений h1 = 25 см и h2 — 75 см. Определите частоту колебаний ν камертона. Скорость звука υ принять равной 340 м/с. Решение. Звучание камертона усиливается в том случае, когда частота свободных колебаний воздушного столба в сосуде совпадает с частотой колебаний камертона. Свободные колебания воздушного столба в закрытой с одного конца трубе соответствуют установлению в ней стоячей волны такой длины λ, что у закрытого конца образуется узел, а у открытого — пучность. Итак, вдоль столба воздуха длиной h укладывается
где k = 0, 1, 2, ... — целые числа. Так как частота колебаний связана с длиной волны формулой
По условию задачи частота имеет вполне определенное значение. Поэтому различным резонансным высотам h1 и h2 воздушного столба должны соответствовать два значения k, отличающиеся на единицу: k1 = n и k2 = n + 1. Это значит, что
|
|
|



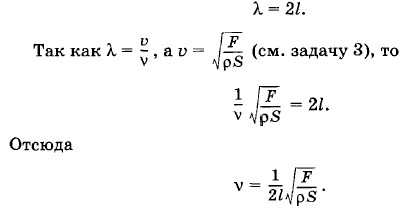
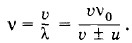
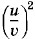
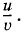 Тогда
Тогда
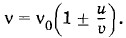
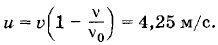
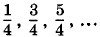 длин волн, т. е. в общем случае
длин волн, т. е. в общем случае
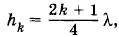
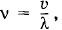 то для соответствующей некоторому значению k частоты камертона получаем:
то для соответствующей некоторому значению k частоты камертона получаем: