|
|
|
|
|
Глава 2. Электромагнитная индукция § 13. ЭДС индукции в движущихся проводникахРассмотрим теперь второй случай возникновения индукционного тока. При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она-то и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение. На многих электростанциях земного шара именно сила Лоренца вызывает перемещение электронов в движущихся проводниках. Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (рис. 2.10). Пусть сторона контура MN длиной I скользит с постоянной скоростью
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю Fл = |q|υ B sin α. (2.5) Направлена эта сила вдоль проводника MN. Работа силы Лоренца1 на пути I положительна и составляет: А = FЛl = |q| υ Bl sin α. 1 Это неполная работа силы Лоренца. Кроме силы Лоренца (см. формулу (2.5)), имеется составляющая силы Лоренца, направленная против скорости и проводника. Эта составляющая тормозит движение проводника и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю. Электродвижущая сила индукции в проводнике MN равна, по определению, отношению работы по перемещению заряда q к этому заряду:
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью В других проводниках контура ЭДС равна нулю, так как эти проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна
|
|
|



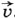 вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции
вдоль сторон NC и MD, оставаясь все время параллельной стороне CD. Вектор магнитной индукции 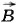 однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.


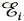 и остается неизменной, если скорость движения
и остается неизменной, если скорость движения