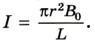|
|
|
|
|
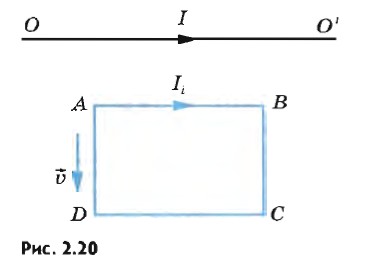
Глава 2. Электромагнитная индукция Электромагнитная индукция: Примеры решения задач1. Прямоугольный контур ABCD перемещается поступательно в магнитном поле тока, идущего по прямолинейному длинному проводнику (рис. 2.20). Определите направление тока, индуцированного в контуре, если контур удаляется от провода. Какие силы действуют на контур?
Р е ш е н и е. Вектор магнитной индукции Взаимодействие тока в контуре с прямолинейным током приводит к появлению сил, действующих на проводники контура. Применив правило левой руки, можно выяснить, что эти силы, во-первых, растягивают рамку, стремясь увеличить площадь контура, и, во-вторых, создают результирующую силу, направленную к прямолинейному проводнику. Оба действия будут препятствовать уменьшению магнитного потока через контур. 2. Кольцо из сверхпроводника помещено в однородное магнитное поле, индукция которого нарастает от нуля до В0. Плоскость кольца перпендикулярна линиям индукции поля. Определите силу индукционного тока, возникающего в кольце. Радиус кольца r, индуктивность L. Р е ш е н и е. Так как сопротивление кольца равно нулю, то и суммарная электродвижущая сила в нем должна быть равна нулю. Иначе сила тока согласно закону Ома станет бесконечной. Следовательно, изменение магнитного потока внешнего магнитного поля равно по модулю и противоположно по знаку изменению магнитного потока, созданного индукционным током: ΔФ = LΔI. Учитывая, что поток Ф0 нарастает от 0 до πr2B0, а сила индукционного тока меняется при этом от 0 до I, получаем πr2B0 = LI. Отсюда
|
|
|



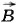 магнитного поля тока I направлен перпендикулярно плоскости контура от нас. При удалении контура от провода магнитный поток через площадку ABCD убывает (ΔФ < 0). Следовательно, вектор магнитной индукции
магнитного поля тока I направлен перпендикулярно плоскости контура от нас. При удалении контура от провода магнитный поток через площадку ABCD убывает (ΔФ < 0). Следовательно, вектор магнитной индукции