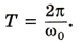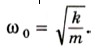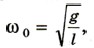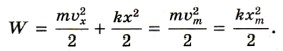|
|
|
|
|
Глава 3. Механические колебания Краткие итоги главы 3: Механические колебания1. Колебания различной природы (механические, электрические и др.) описываются одинаковыми уравнениями. Различают свободные, затухающие и вынужденные колебания. 2. Свободные колебания возникают в системе под влиянием внутренних сил после того, как она выведена из состояния равновесия. С течением времени свободные колебания вследствие трения затухают. 3. Вынужденные колебания возникают при действии на систему внешней периодической силы. Эти колебания не затухают до тех пор, пока действует внешняя сила. Пример вынужденных колебаний: раскачивание качелей с помощью периодических толчков. 4. Свободные колебания груза, прикрепленного к пружине, можно описать вторым законом Ньютона. Его следствием применительно к данному случаю является уравнение
где х — смещение груза от положения равновесия; х" — ускорение груза; 5. Решение уравнения, описывающего свободные колебания, выражается через косинус: х = хm cos (ω0t + φ0) — или синус. Колебания, происходящие по закону косинуса или синуса, называются гармоническими. 6. Модуль максимального смещения тела хm от положения равновесия называется амплитудой колебаний. Величина ω0 называется циклической частотой колебаний и выражается через частоту колебаний ν так: ω0 = 2πν. 7. Промежуток времени, за который система совершает одно полное колебание, называется периодом колебаний. Период можно выразить через циклическую частоту:
8. Величину, стоящую под знаком косинуса или синуса, называют фазой колебаний. Фаза определяет положение колеблющегося тела в произвольный момент времени при заданной амплитуде колебаний. 9. Собственная циклическая частота колебаний груза, прикрепленного к пружине, зависит от его массы m и жесткости пружины k:
Собственная циклическая частота колебаний математического маятника определяется формулой
где g — ускорение свободного падения, а l — длина маятника. Частота (как и период) гармонических колебаний не зависит от амплитуды. 10. Энергия колеблющегося тела при отсутствии сил трения сохраняется:
Вынужденные колебания совершаются при воздействии на систему, в которой могут происходить колебания, периодической силы. При этом может наблюдаться резонанс: резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы с собственной частотой колебаний системы. Резонанс проявляется отчетливо лишь в системах с малым трением.
|
|
|



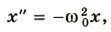
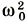 — постоянная, зависящая от свойств системы.
— постоянная, зависящая от свойств системы.