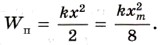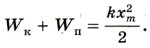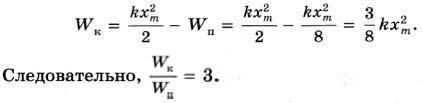|
|
|
|
|
Глава 3. Механические колебания Механические колебания: Примеры решения задач1. Сколько колебаний совершает математический маятник длиной l = 4,9 м за время t = 5 мин? Р е ш е н и е. Период колебаний определяется по формуле
Искомое число колебаний можно найти так:
2. Вертикально подвешенная пружина растягивается прикрепленным к ней грузом на Δl = 0,8 см. Чему равен период Т свободных колебаний груза? (Массой пружины пренебречь.) Р е ш е н и е. Период колебаний груза, прикрепленного к пружине, определяется формулой
где m — масса груза; k — жесткость пружины. На груз действуют сила тяжести FT = Fynp. Так как FT = mg и Fynp = k Δl (закон Гука), то mg = kΔl, откуда Следовательно,
3. На горизонтальном стержне находится груз, прикрепленный к пружине (см. рис. 3.3). Другой конец пружины закреплен. В некоторый момент времени груз смещают от положения равновесия на хm = 10 см и отпускают. Определите координату груза спустя 1/8 периода колебаний. (Трение не учитывать.) Р е ш е н и е. Зависимость координаты груза от времени выражается так: x = xm cos ω0t.
4. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне (см. рис. 3.3). Определите отношение кинетической энергии груза к потенциальной энергии системы в момент, когда груз находится в точке, расположенной посредине между крайним положением и положением равновесия. Р е ш е н и е. Координата указанной точки равна половине амплитуды колебаний:
В любой момент времени выполняется равенство
Поэтому кинетическая энергия груза в момент прохождения им указанной точки определяется так:
|
|
|



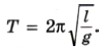
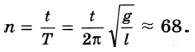

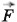 T и сила упругости
T и сила упругости 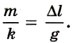
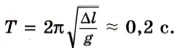
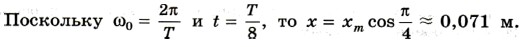
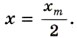 Потенциальная энергия системы в момент прохождения груза через эту точку равна:
Потенциальная энергия системы в момент прохождения груза через эту точку равна: