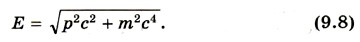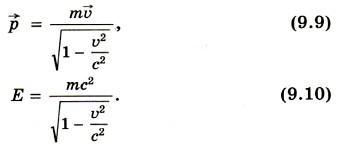|
|
|
|
|
Глава 9. Элементы теории относительности § 79. Элементы релятивистской динамикиС новыми пространственно-временными представлениями не согласуются при больших скоростях движения и законы механики Ньютона. Лишь при малых скоростях движения, когда справедливы классические представления о пространстве и времени, второй закон Ньютона (уравнение движения)
не меняет своей формы при переходе от одной инерциальной системы отсчета к другой (выполняется принцип относительности). Но при больших скоростях движения этот закон в своей обычной (классической) форме несправедлив. Однако введенные в динамике основные понятия: энергия, импульс — имеют тот же физический смысл, лишь понятие массы в классической механике отличается от понятия массы в релятивистской динамике. В природе существуют частицы, скорость которых равна скорости света. Это фотоны и различного типа нейтрино. Масса этих частиц равна нулю. Они не могут быть замедлены или ускорены. Поэтому во всех инерциальных системах отсчета их импульс и энергия не равны нулю. Такие частицы называются безмассовыми. Энергия и импульс таких частиц связаны соотношениями Е = рс и Е2 - р2с2 = 0. (9.5) Эти соотношения экспериментально подтверждены. Однако для большинства частиц масса является одной из важнейших характеристик. Эти частицы называются массовыми. Скорость таких частиц υ < с. Массовая частица обладает собственной энергией: Е = mс2. (9.6) Согласно этой формуле тело обладает энергией и при скорости, равной нулю — энергией покоя. Это замечательный результат. Любое тело уже только благодаря факту своего существования обладает энергией, которая пропорциональна его массе m. При превращениях элементарных частиц, обладающих массой покоя m ≠ 0, в частицы, у которых m = 0, их энергия покоя Е0 целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя. Во всех инерциальных системах отсчета импульс частицы и ее энергия связаны соотношением: Е2 - р2с2 = m2с4. (9.7) Так как величины m и с не меняются при переходе от одной системы отсчета к другой, то, следовательно, не меняется и значение Е2 - р2с2. Выражение (9.7) преобразуется в уравнение (9.5) при m = 0, следовательно, оно справедливо также и для безмассовых частиц. Формула (9.7) является фундаментальным соотношением релятивистской механики. Энергия частицы выражается через ее импульс следующим образом:
Используя формулу (9.8), а также учитывая, что импульс частицы пропорционален ее скорости и энергии, получаем выражения для импульса и энергии частицы:
|
|
|