|
|
|
|
|
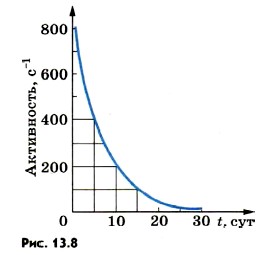
Глава 13. Физика атомного ядра § 101. Закон радиоактивного распада. Период полураспадаРадиоактивный распад подчиняется статистическому закону. Резерфорд, исследуя превращения радиоактивных веществ, установил опытным путем, что их активность убывает с течением времени. Об этом говорилось в предыдущем параграфе. Так, активность радона убывает в 2 раза уже через 1 мин. Активность таких элементов, как уран, торий и радий, тоже убывает со временем, но гораздо медленнее. Для каждого радиоактивного вещества существует определенный интервал времени, на протяжении которого активность убывает в 2 раза. Этот интервал носит название период полураспада. Период полураспада Т — это время, в течение которого распадается половина начального числа радиоактивных атомов. Спад активности, т. е. числа распадов в секунду, в зависимости от времени для одного из радиоактивных препаратов изображен на рисунке 13.8. Период полураспада этого вещества равен 5 сут.
Выведем теперь математическую форму закона радиоактивного распада. Пусть число радиоактивных атомов в начальный момент времени (t = 0) равно N0. Тогда по истечении периода полураспада это число будет равно Спустя еще один такой же интервал времени это число станет равным:
По истечении времени t = nТ, т. е. спустя n периодов полураспада Т, радиоактивных атомов останется:
Поскольку
то
Это и есть основной закон радиоактивного распада. По формуле (13.1) можно найти число нераспавшихся ядер в любой момент времени. Период полураспада — основная величина, определяющая скорость радиоактивного распада. Чем меньше период полураспада, тем меньше времени «живут» ядра, тем быстрее происходит распад. Для разных веществ период полураспада имеет сильно различающиеся значения. Так, период полураспада урана Чтобы, пользуясь формулой (13.1), определить период полураспада, надо знать число атомов N0 в начальный момент времени и число нераспавшихся атомов N спустя определенный интервал времени t. Сам закон радиоактивного распада довольно прост. Но физический смысл этого закона уяснить себе нелегко. Действительно, согласно этому закону за любой интервал времени распадается одна и та же доля имеющихся атомов (за период полураспада половина атомов). Значит, с течением времени скорость распада нисколько не меняется? Радиоактивные ядра «не стареют». Так, ядра радона, возникающие при распаде радия, претерпевают радиоактивный распад как сразу же после своего образования, так и спустя 10 мин после этого. Распад любого атомного ядра — это, так сказать, не «смерть от старости», а «несчастный случай» в его жизни. Для радиоактивных ядер не существует понятия возраста. Можно определить лишь их среднее время жизни τ. Время существования отдельных ядер может варьироваться от долей секунды до миллиардов лет. Атом урана, например, может спокойно пролежать в земле миллиарды лет и внезапно взорваться, тогда как его соседи благополучно продолжают оставаться в прежнем состоянии. Среднее время жизни τ — это просто среднее арифметическое времени жизни достаточно большого количества атомов данного вида. Оно прямо пропорционально периоду полураспада. Предсказать, когда произойдет распад ядра данного атома, невозможно. Смысл имеют только утверждения о поведении в среднем большой совокупности атомов. Закон радиоактивного распада определяет среднее число ядер атомов, распадающихся за определенный интервал времени. Но всегда имеются неизбежные отклонения от среднего значения, и, чем меньше количество радиоактивных ядер в препарате, тем больше эти отклонения. Закон радиоактивного распада является статистическим законом. Говорить об определенном законе радиоактивного распада для малого числа ядер атомов не имеет смысла. Этот закон справедлив в основном для большого количества частиц. Вопрос к параграфу Счетчик регистрирует β-частицы радиоактивного препарата очень малой интенсивности. Происходят ли срабатывания счетчика через одинаковые интервалы времени?
|
|
|



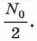
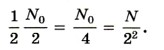
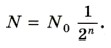
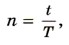

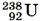 равен 4,5 млрд лет. Именно поэтому активность урана на протяжении нескольких лет заметно не меняется. Период полураспада радия значительно меньше — он равен 1600 лет. Поэтому активность радия значительно больше активности урана. Есть радиоактивные элементы с периодом полураспада в миллионные доли секунды.
равен 4,5 млрд лет. Именно поэтому активность урана на протяжении нескольких лет заметно не меняется. Период полураспада радия значительно меньше — он равен 1600 лет. Поэтому активность радия значительно больше активности урана. Есть радиоактивные элементы с периодом полураспада в миллионные доли секунды.